题目内容
(2007
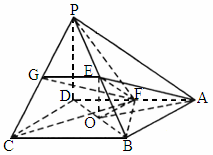
北京东城模拟)如下图,在四棱锥P—ABCD中,底面ABCD为正方形,PD⊥平面ABCD,且PD=AB=2,E是PB的中点,F是AD的中点.(1)
求异面直线PD与AE所成角的大小;(2)
求证:EF⊥平面PBC;(3)
求二面角F—PC—B的大小.
答案:略
解析:
解析:
|
解析:连接 BD,∵PD⊥平面ABCD,∴平面 PDB⊥平面ABCD.过点 E作EO⊥BD于O,连接AO.则 EO∥PD,且EO⊥平面ABCD.∴∠ AEO为异面直线PD,AE所成的角∵ E是PB的中点,则O是BD的中点,且 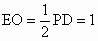 . .
在 Rt△EOA中,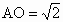 , ,
∴ 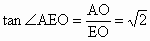 . .
即异面直线 PD与AE所成角的大小为 . .
(2) 连接FO.∵F是AD的中点,∴ OF⊥AD.∵EO⊥平面ABCD,由三垂线定理,得 EF⊥AD.又∵ AD∥BC,∴EF⊥BC.连接FB.可求得 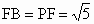 .则EF⊥PB. .则EF⊥PB.
又∵ PB∩BC=B,∴EF⊥平面PBC(3) 取PC的中点G,连接EG,FG.则 EG是FG在平面PBC内的射影.∵ PD⊥平面ABCD,∴PD⊥BC.又 DC⊥BC,且PD∩DC=D,∴ BC⊥平面PDC.∴BC⊥PC.∵ EG∥BC,则EG⊥PC.∴FG⊥PC.∴∠ FGE是二面角F-PC-B的平面角.在 Rt△FEG中,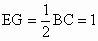 , ,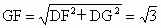 , ,
∴  . .
∴二面角 F-PC-B的大小为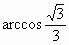 . . |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 有且仅有一个解
有且仅有一个解
 ”,它对于正整数n满足以下运算性质:
”,它对于正整数n满足以下运算性质:
 1001=1
1001=1 ,则2008
,则2008 1001的值是________.
1001的值是________. 的图象与直线ex+y=0相切于点A,且点A的横坐标为1.
的图象与直线ex+y=0相切于点A,且点A的横坐标为1.
 的各项均为正数,
的各项均为正数, 为其前n项和,对于任意
为其前n项和,对于任意 ,满足关系
,满足关系 .
.
 的通项公式;
的通项公式;
 的前n项和为
的前n项和为 ,且
,且 ,求证:对任意正整数n,总有
,求证:对任意正整数n,总有 ;
;
 中,设
中,设 ,求数列
,求数列 中的最大项.
中的最大项.