题目内容
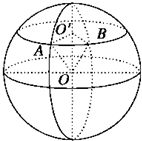 设地球的半径为R,地球上的两点A、B的纬度都是北纬45°,A、B两点间的距离为R,已知A在东经20°处,试确定B点的位置.
设地球的半径为R,地球上的两点A、B的纬度都是北纬45°,A、B两点间的距离为R,已知A在东经20°处,试确定B点的位置.分析:由A、B的球面距离是指过A、B的大圆的劣弧长,知∠AOB=60°,AB=R,再由O′A=OA•cos45°=R,推导出A、B两点的经度差是90°.由此能确定B点的位置.
解答:解:如图,因为A、B的球面距离是指过A、B的大圆的劣弧长,
所以∠AOB=60°,因此AB=R,
又O′A=OA•cos45°=R,
在△AO′B中,AO′=BO′=R,AB=R,
∴AB2=AO′2+BO′2,∠AO′B=90°,
即A、B两点的经度差是90°.
因为A在东经20°处,所以B点的位置在20°±90°处,
即B点位于北纬45°东经110°,或北纬45°西经70°处.

所以∠AOB=60°,因此AB=R,
又O′A=OA•cos45°=R,
在△AO′B中,AO′=BO′=R,AB=R,
∴AB2=AO′2+BO′2,∠AO′B=90°,
即A、B两点的经度差是90°.
因为A在东经20°处,所以B点的位置在20°±90°处,
即B点位于北纬45°东经110°,或北纬45°西经70°处.
点评:本题考查球面距离的计算及其应用,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
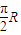 ,若A地为东经0°,则B地的经度为 .
,若A地为东经0°,则B地的经度为 .