题目内容
已知函数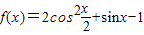
(1)求函数f(x)的最小正周期和值域;
(2)若
 ,且
,且 ,求sinx的值.
,求sinx的值.
【答案】分析:(1)函数解析式第一、三项结合,利用二倍角的余弦函数公式化简,整理后再利用两角和与差的余弦函数公式化为一个角的余弦函数,找出ω的值,代入周期公式求出f(x)的最小正周期;由余弦函数的值域即可求出函数的值域;
(2)由x的范围求出这个角的范围,由f(x)= ,求出cos(x-
,求出cos(x-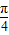 )的值,利用同角三角函数间的基本关系求出sin(x-
)的值,利用同角三角函数间的基本关系求出sin(x-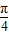 )的值,将sinx中的x变形为(x-
)的值,将sinx中的x变形为(x-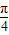 )+
)+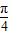 ,利用两角和与差的正弦函数公式及特殊角的三角函数值化简后,将各自的值代入即可求出值.
,利用两角和与差的正弦函数公式及特殊角的三角函数值化简后,将各自的值代入即可求出值.
解答:解:(1)∵f(x)=cosx+sinx=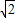 cos(x-
cos(x-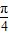 ),
),
∴函数f(x)的周期为2π,
又∵-1≤cos(x-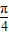 )≤1,
)≤1,
则函数f(x)的值域为[-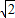 ,
,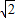 ];
];
(2)∵f(x)=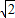 cos(x-
cos(x-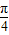 )=
)= ,
,
∴cos(x-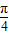 )=
)=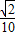 ,
,
∵x∈(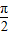 ,
,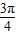 ),∴x-
),∴x-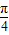 ∈(
∈(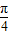 ,
,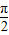 ),
),
∴sin(x-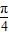 )=
)=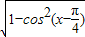 =
=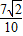 ,
,
则sinx=sin[(x-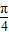 )+
)+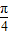 ]=sin(x-
]=sin(x-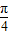 )cos+cos(x-
)cos+cos(x-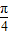 )sin
)sin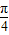
=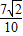 ×
× +
+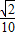 ×
×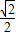 =
= .
.
点评:此题考查了两角和与差的正弦函数公式,同角三角函数间的基本关系,余弦函数的定义域与值域,以及三角函数的周期性及其求法,熟练掌握公式是解本题的关键.
(2)由x的范围求出这个角的范围,由f(x)=
 ,求出cos(x-
,求出cos(x-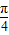 )的值,利用同角三角函数间的基本关系求出sin(x-
)的值,利用同角三角函数间的基本关系求出sin(x-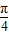 )的值,将sinx中的x变形为(x-
)的值,将sinx中的x变形为(x-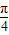 )+
)+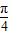 ,利用两角和与差的正弦函数公式及特殊角的三角函数值化简后,将各自的值代入即可求出值.
,利用两角和与差的正弦函数公式及特殊角的三角函数值化简后,将各自的值代入即可求出值.解答:解:(1)∵f(x)=cosx+sinx=
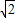 cos(x-
cos(x-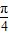 ),
),∴函数f(x)的周期为2π,
又∵-1≤cos(x-
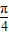 )≤1,
)≤1,则函数f(x)的值域为[-
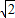 ,
,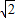 ];
];(2)∵f(x)=
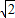 cos(x-
cos(x-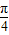 )=
)= ,
,∴cos(x-
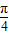 )=
)=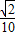 ,
,∵x∈(
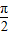 ,
,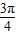 ),∴x-
),∴x-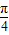 ∈(
∈(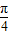 ,
,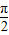 ),
),∴sin(x-
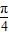 )=
)=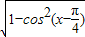 =
=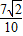 ,
,则sinx=sin[(x-
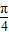 )+
)+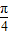 ]=sin(x-
]=sin(x-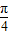 )cos+cos(x-
)cos+cos(x-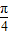 )sin
)sin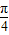
=
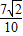 ×
× +
+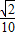 ×
×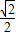 =
= .
.点评:此题考查了两角和与差的正弦函数公式,同角三角函数间的基本关系,余弦函数的定义域与值域,以及三角函数的周期性及其求法,熟练掌握公式是解本题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目



 的极值点;
的极值点; 过点(0,—1),并且与曲线
过点(0,—1),并且与曲线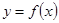 相切,求直线
相切,求直线 ,其中
,其中 ,求函数
,求函数 在
在 上的最小值.(其中e为自然对数的底数)
上的最小值.(其中e为自然对数的底数)