题目内容
已知M(4,0),N(1,0)若动点P满足
•
=6|
|
(1)求动点P的轨迹方C的方程;
(2)设Q是曲线C上任意一点,求Q到直线l:x+2y-12=0的距离的最小值.
| MN |
| MP |
| NP |
(1)求动点P的轨迹方C的方程;
(2)设Q是曲线C上任意一点,求Q到直线l:x+2y-12=0的距离的最小值.
分析:(1)设动点P(x,y),则由已知P满足
•
=6|
|可知P的轨迹方程
(2)解法一:由几何性质意义知,椭圆C与平行的切线其中一条和l的距离等于Q与l的距离的最小值.
把x+2y+D=0代入椭圆方程消去x,由△=0可得D,进而可求最小距离
解二:由集合意义知,椭圆C与平行的切线其中一条l′和l的距离等于Q与l的距离的最小值.设切点为R(x0,y0),则l′:
+
=1,且
+
=1,k=-
=-
,联立可求x0,y0,代入可求最小距离
解三:由椭圆参数方程设Q(2cosθ,
sinθ),由点Q与l距离d=
=
,结合三角函数的性质可求
解四:设Q(x0,y0),
+
=1且Q与l距离d=
,由柯西不等式可求
| MN |
| MP |
| NP |
(2)解法一:由几何性质意义知,椭圆C与平行的切线其中一条和l的距离等于Q与l的距离的最小值.
把x+2y+D=0代入椭圆方程消去x,由△=0可得D,进而可求最小距离
解二:由集合意义知,椭圆C与平行的切线其中一条l′和l的距离等于Q与l的距离的最小值.设切点为R(x0,y0),则l′:
| x0x |
| 4 |
| y0y |
| 3 |
| ||
| 4 |
| ||
| 3 |
| 3x0 |
| 4y0 |
| 1 |
| 2 |
解三:由椭圆参数方程设Q(2cosθ,
| 3 |
|2cosθ+2
| ||
|
| 12-4sin(θ+30°) | ||
|
解四:设Q(x0,y0),
| ||
| 4 |
| ||
| 3 |
| |x0+2y0-12| | ||
|
解答:解:(1)设动点P(x,y),则
(x-4,y),
=(-3,0),
=(1-x,-y)
由已知得-3(x-4)=6
,化简得3x2+4y2=12即
+
=1
∴点P的轨迹方程是椭圆C:
+
=1
(2)解一:由几何性质意义知,椭圆C与平行的切线其中一条l‘和l的距离等于Q与l的距离的最小值.
设l′:x+2y+D=0
代入椭圆方程消去x化简得:16y2+12Dy+3(D2-4)=0∴△=144D2-192(D2-4)=0⇒D=±4
l′与l距离的最小值为
∴Q与l距离的最小值为
解二:由集合意义知,椭圆C与平行的切线其中一条l‘和l的距离等于Q与l的距离的最小值.设切点为R(x0,y0),则l′:
+
=1,且
+
=1k=-
=-
解得
或
∴l′为x+2y±4=0
l′与l距离的最小值为
∴Q与l距离的最小值为
解三:由椭圆参数方程设Q(2cosθ,
sinθ)
则Q与l距离d=
=
∴sin(θ+30°)=1时dmin=
=
解四:设Q(x0,y0),
+
=1
且Q与l距离d=
由柯西不等式16=(
+
)(4+12)≥(
•2+
•2
)2=(x0+2y0)2,
∴|x0+2y0|≤4,
∴dmin=
=
| MP |
| MN |
| PN |
由已知得-3(x-4)=6
| (1-x)2+(-y)2 |
| x2 |
| 4 |
| y2 |
| 3 |
∴点P的轨迹方程是椭圆C:
| x2 |
| 4 |
| y2 |
| 3 |
(2)解一:由几何性质意义知,椭圆C与平行的切线其中一条l‘和l的距离等于Q与l的距离的最小值.
设l′:x+2y+D=0
代入椭圆方程消去x化简得:16y2+12Dy+3(D2-4)=0∴△=144D2-192(D2-4)=0⇒D=±4
l′与l距离的最小值为
| |12±4| | ||
|
∴Q与l距离的最小值为
8
| ||
| 5 |
解二:由集合意义知,椭圆C与平行的切线其中一条l‘和l的距离等于Q与l的距离的最小值.设切点为R(x0,y0),则l′:
| x0x |
| 4 |
| y0y |
| 3 |
| ||
| 4 |
| ||
| 3 |
| 3x0 |
| 4y0 |
| 1 |
| 2 |
解得
|
|
l′与l距离的最小值为
| |12±4| | ||
|
∴Q与l距离的最小值为
8
| ||
| 5 |
解三:由椭圆参数方程设Q(2cosθ,
| 3 |
则Q与l距离d=
|2cosθ+2
| ||
|
| 12-4sin(θ+30°) | ||
|
| 12-4 | ||
|
8
| ||
| 5 |
解四:设Q(x0,y0),
| ||
| 4 |
| ||
| 3 |
且Q与l距离d=
| |x0+2y0-12| | ||
|
由柯西不等式16=(
| ||
| 4 |
| ||
| 3 |
| x0 |
| 2 |
| y0 | ||
|
| 3 |
∴|x0+2y0|≤4,
∴dmin=
| 12-4 | ||
|
8
| ||
| 5 |
点评:本题以向量的数量积的定义为载体,主要考查了直线与椭圆的位置关系的应用,注意体会了一题多解 的方法的应用.

练习册系列答案
相关题目
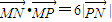 .
.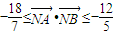 ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.