题目内容

19．设集合A={x|0≤x≤2}，B={x|x≥a}，若A⊆B，则a的取值范围是（　　）
A．a≤0B．a＜0C．a＜2D．a≤2

分析 由题意在数轴上作出集合A，B，从而解得．

解答 解：∵集合A={x|0≤x≤2}，B={x|x≥a}，
根据A⊆B作图如下，

结合图象可得，
a≤0，
故选A．

点评 本题考查了集合包含关系的应用，属于基础题．

练习册系列答案
相关题目
8．已知f（x）=lnx-ax2-bx．记f（x）的导函数是f′（x）．
（Ⅰ）若a=-1，函数f（x）在其定义域内是增函数，求b的取值范围；
（Ⅱ） f（x）的图象与x轴交于A（x1，0），B（x2，0）（x1＜x2））两点，AB中点为C（x0，0），求证：f′（x0）＜0．
10．已知O为坐标原点，F为抛物线C：y2=4$\sqrt{6}$x的焦点，P为C上一点，若△POF的面积为6$\sqrt{3}$，则|PF|=（　　）
A．$2\sqrt{3}$B．$4\sqrt{3}$C．$4\sqrt{6}$D．$8\sqrt{3}$
7．已知椭圆的中心是坐标原点O，焦点在x轴上，离心率为$\frac{\sqrt{2}}{2}$，坐标原点O到过右焦点F且斜率为1的直线的距离为$\frac{\sqrt{2}}{2}$．
（1）求椭圆的标准方程；
（2）设过右焦点F且与坐标轴不垂直的直线l交椭圆于P、Q两点，在线段OF上是否存在点M（m，0），使得|MP|=|MQ|？若存在，求出m的取值范围；若不存在，请说明理由．
14．若曲线C上的点到椭圆 $\frac{{x}^{2}}{1{3}^{2}}$+$\frac{{y}^{2}}{1{2}^{2}}$=1的两个焦点的距离的差的绝对值等于8，则曲线C的标准方程为（　　）
A．$\frac{{x}^{2}}{1{3}^{2}}$-$\frac{{y}^{2}}{1{2}^{2}}$=1B．$\frac{{x}^{2}}{1{3}^{2}}$-$\frac{{y}^{2}}{{5}^{2}}$=1
C．$\frac{{x}^{2}}{{3}^{2}}$-$\frac{{y}^{2}}{{4}^{2}}$=1D．$\frac{{x}^{2}}{{4}^{2}}$-$\frac{{y}^{2}}{{3}^{2}}$=1
4．执行如图所示的程序框图，若结束时输出的结果不小于3，则t的取值范围为（　　）
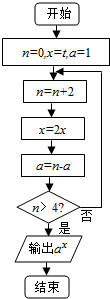
A．[$\frac{1}{4}$，+∞）B．[$\frac{1}{8}$，+∞）C．（-∞，$\frac{1}{8}$]D．（-$∞，\frac{1}{4}$]
11．如图，在公路MN的两侧有四个村镇：A1、B1、C1、D1通过小路和公路相连，各路口分别是A、B、C、D，现要在公路上建一个长途汽车站，为使各村镇村民到汽车站所走的路程总和最小，汽车站应建在（　　）
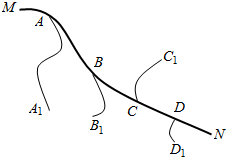
A．A处B．D处
C．B、C间的任何一处（包括B、C）D．A、B之间的任何一处（包括A、B）
8．为了预测某射手的射击水平，设计了如下的模拟实验，通过实验产生了20组随机数：
6830   3018  7055   7430   7740   4422  7884   2604   3346   0952 
6807   9706   5774   5725   6576  5929   9768   6071  9138   6754
如果一组随机数中恰有三个数在1，2，3，4，5，6中，表示四次射击中恰有三次击中目标的概率约为 （　　）
A．25%B．20%C．30%D．50%
9．阅读程序图，该程序图输出的结果是（　　）
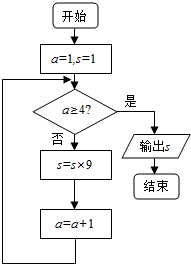
A．94B．92C．95D．93

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网