题目内容
顶点在原点，焦点在x轴上的抛物线被直线2x-y+1=0截得的弦长为
,求抛物线方程.
解析：设抛物线方程为y2=2px或y2=-2px,由方程组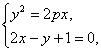得4x2+(4-2p)x+1=0,则x1+x2=
(p-2),x1·x2=
，同样由方程组可得y2-py+p=0,则y1+y2=p,y1·y2=p.那么由
=
(
)2-1+p2-4p=15
p=6,则得方程为y2=12x.当抛物线为y2=-2px时同样可求出p=2,∴y2=-4x.故所求方程为y2=12x或y2=-4x.
练习册系列答案
相关题目
已知直线l过坐标原点，抛物线C顶点在原点，焦点在x轴正半轴上．若点A（-1，0）和点B（0，8）关于l的对称点都在C上，求直线l和抛物线C的方程．顶点在原点、焦点在x轴上的抛物线被直线y=x+1截得的弦长是
，则抛物线的方程是（ ）
| 10 |
| A、y2=-x或y2=5x |
| B、y2=-x |
| C、y2=x或y2=-5x |
| D、y2=5x |