题目内容
设椭圆的中心在原点,焦点在x轴上,离心率e=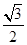 .已知点P
.已知点P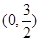 到这个椭圆上的点的最远距离为
到这个椭圆上的点的最远距离为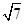 ,求这个椭圆的方程.
,求这个椭圆的方程.
【答案】
设椭圆方程为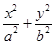 =1(a>b>0),M(x,y)为椭圆上的点,由
=1(a>b>0),M(x,y)为椭圆上的点,由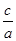 =
=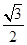 得a=2b.
得a=2b.
|PM|2=x2+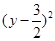 =-3
=-3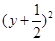 +4b2+3(-b≤y≤b),
+4b2+3(-b≤y≤b),
若b<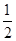 ,则当y=-b时,|PM|2最大,即
,则当y=-b时,|PM|2最大,即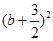 =7,
=7,
则b=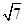 -
-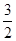 >
>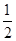 ,故舍去.
,故舍去.
若b≥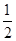 时,则当y=-
时,则当y=-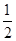 时,|PM|2最大,即4b2+3=7,
时,|PM|2最大,即4b2+3=7,
解得b2=1.
∴所求方程为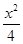 +y2=1.
+y2=1.
【解析】略

练习册系列答案
相关题目
 设椭圆的中心在原点,坐标轴为对称轴,焦点在x轴上,一个焦点与短轴两端点的连线互相垂直,且此焦点与长轴上较近的端点距离为
设椭圆的中心在原点,坐标轴为对称轴,焦点在x轴上,一个焦点与短轴两端点的连线互相垂直,且此焦点与长轴上较近的端点距离为