题目内容
已知F1、F2分别是椭圆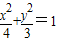 的左、右焦点,点M在椭圆上且MF2⊥x轴,则|MF1|等于( )
的左、右焦点,点M在椭圆上且MF2⊥x轴,则|MF1|等于( )A.

B.

C.

D.3
【答案】分析:利用MF2⊥x轴,即可得出点M的坐标,再利用椭圆的定义即可得出.
解答:解:由椭圆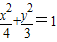 可得a2=4,b2=3,∴
可得a2=4,b2=3,∴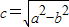 =1,
=1,
∵MF2⊥x轴,可设M(1,yM),则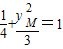 ,解得yM=
,解得yM= .
.
∴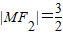 .
.
∵|MF2|+|MF1|=4,
∴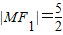 .
.
故选C.
点评:熟练掌握椭圆的定义是解题的关键.
解答:解:由椭圆
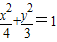 可得a2=4,b2=3,∴
可得a2=4,b2=3,∴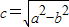 =1,
=1,∵MF2⊥x轴,可设M(1,yM),则
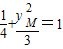 ,解得yM=
,解得yM= .
.∴
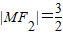 .
.∵|MF2|+|MF1|=4,
∴
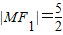 .
.故选C.
点评:熟练掌握椭圆的定义是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,已知F1,F2分别是椭圆C:
如图,已知F1,F2分别是椭圆C: