题目内容
.(本小题满分12分)
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,AB=2,AC=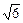
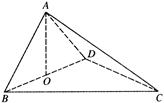
(1)求证:AO⊥平面BCD;
(2)求二面角A—BC—D的余弦值;
(3)求点O到平面ACD的距离.
解法一:(1)连接OC, n·
∵△ABD和△CBD为等边三角形,O为BD的中点,
∴AO⊥BD,CO⊥BD,又AB=2,AC=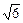 ,
,
∴AO= CO=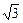 .…………………………3分
.…………………………3分
在△AOC中,∵AO2+ CO2= AC2,
∴∠AOC=90o,即AO⊥OC.
∵BD∩OC=O,∴AO⊥平面BCD.………………4分
(2)过O作OE⊥BC于E,连接AE,∵AO⊥平面BCD,
∴AE在平面BCD上的射影为OE,∴AE⊥BC,
∴∠AEO为二面角A—BC—D的平面角.………………6分
在Rt△AEO中,AO=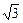 ,OE=
,OE=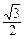 ,
,
tan∠AEO=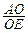 =2,cos∠AEO=
=2,cos∠AEO=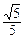 ,
,
∴二面角A—BC—D的余弦值为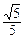 .……………………8分
.……………………8分
(3)设点O到平面ACD的距离为h.
∵VO—ACD= VA—OCD,∴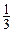 S
S △ACD·h—=
△ACD·h—=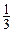 S△OCD·AO.
S△OCD·AO.
在△ACD中,AD= CD=2,AC=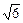 ,
,
S△ACD=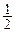
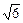 ·
·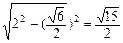 .
.
而AO=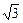 ,S△OCD=
,S△OCD=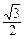 ,
,
∴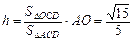 ,
,
∴点O到平面ACD的距离为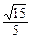 .…………………………12分
.…………………………12分
解法二:(1)同解法一.……………………………………4分
(2)以O为原点,如图建立空间直角坐标系,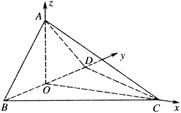
则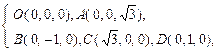 …………5分
…………5分
∵AO⊥平面BCD,
∴平面BCD的法向量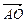 =(0,0,
=(0,0,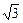 )…………6分
)…………6分
设平面ABC的法向量n=(x,y,z),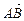 =(0,-1,-
=(0,-1,-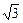 ),
),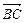 =(
=(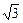 ,1,0).
,1,0).
由n·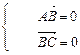
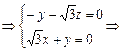 n=(1,-
n=(1,-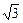 ,1).
,1).
|
|
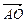 的夹角为
的夹角为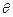 ,则|cos
,则|cos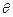 |=
|=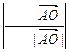 =
=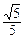 ,
,  ∴二面角A—BC—D的余弦值为
∴二面角A—BC—D的余弦值为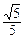 .…………………………8分
.…………………………8分(3)设平面ACD的法向量m=(x,y,z),
|
|
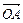 与m的夹角为
与m的夹角为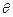 ,则|cos
,则|cos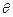 |=
|=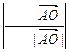 =
=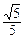 . 设点O到平面ACD的距离为h,
. 设点O到平面ACD的距离为h,∵
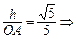 h=
h=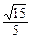 ,
,∴点O到平面ACD的距离为
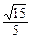 .…………………………12分
.…………………………12分
解析

练习册系列答案
相关题目