题目内容
已知
(Ⅰ)当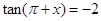 时,求
时,求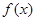 的值;
的值;
(Ⅱ)指出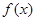 的最大值与最小值,并分别写出使
的最大值与最小值,并分别写出使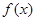 取得最大值、最小值的自变量
取得最大值、最小值的自变量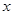 的集合.
的集合.
【答案】
(1)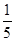 ;(2)最大值1,
;(2)最大值1,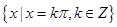 ;最小值0,
;最小值0,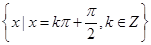 .
.
【解析】本试题主要考查了三角函数中诱导公式的、同角三角关系式的运用,以及正余弦函数的最值的求解和运算的综合试题。诱导公式符合奇变偶不变符号看象限的原则,是化简的关键步骤。
解: (Ⅰ)
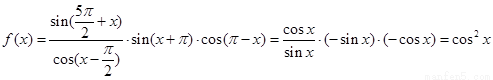
……………………3分
由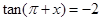 ,得
,得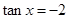 .
……………………4分
.
……………………4分
所以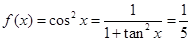 .
……………………6分
.
……………………6分
(Ⅱ)因为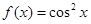 ,所以
,所以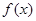 的最大值为1,最小值为0. …………8分
的最大值为1,最小值为0. …………8分
当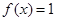 时,
时,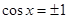 ,此时
,此时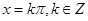 .
.
所以使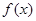 取得最大值的自变量
取得最大值的自变量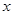 的集合为
的集合为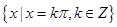 .
.
……………………10分
当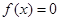 时,
时,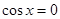 ,此时
,此时 .
.
所以使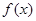 取得最小值的自变量
取得最小值的自变量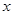 的集合为
的集合为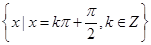 .………12分
.………12分

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
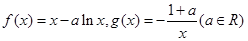 .
. 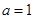 时,求曲线
时,求曲线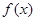 在
在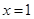 处的切线方程;
处的切线方程;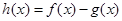 ,求函数
,求函数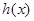 的单调区间;
的单调区间;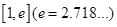 上存在一点
上存在一点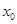 ,使得
,使得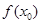 <
<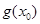 成立,求
成立,求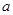 的取值范围.
的取值范围.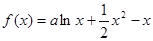
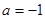 时,求函数
时,求函数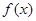 的单调区间;
的单调区间;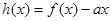 ,对定义域内任意x,均有
,对定义域内任意x,均有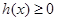 恒成立,求实数a的取值范围?
恒成立,求实数a的取值范围?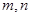 ,
,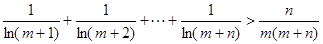 恒成立。
恒成立。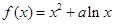 .
.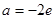 时,求函数
时,求函数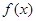 的单调区间和极值;
的单调区间和极值;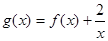 在区间
在区间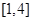 上是单调递减函数,求实数
上是单调递减函数,求实数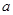 的取值范围.
的取值范围. 
 时,求
时,求 的单调区间;
的单调区间; ,
,  恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.