题目内容
已知函数
(Ⅰ)当 时,求
时,求 的单调区间;
的单调区间;
(Ⅱ)若对任意 ,
,  恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
【答案】
(Ⅰ)单调递增区间为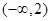 ,单调递减区间为
,单调递减区间为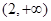 .(Ⅱ)
.(Ⅱ)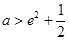
【解析】
试题分析:(Ⅰ)当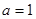 时,
时,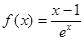
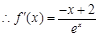 ………………………………………………………………2分 由
………………………………………………………………2分 由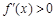 得
得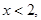
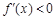 得
得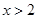
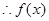 的单调递增区间为
的单调递增区间为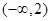 ,单调递减区间为
,单调递减区间为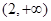 .………………4分
.………………4分
(Ⅱ)若对任意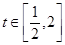 , 使得
, 使得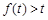 恒成立, 则
恒成立, 则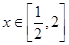 时,
时,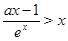 恒成立,
恒成立,
即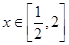 时,
时,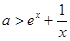 恒成立………………………………6分
恒成立………………………………6分
设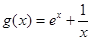 ,
, ,则
,则 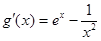 ,
,
设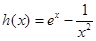 ,
, 
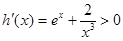 在
在 上恒成立
上恒成立
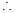
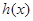 在
在 上单调递增
上单调递增
即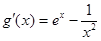 在
在 上单调递增………………8分
上单调递增………………8分
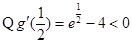 ,
,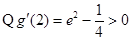
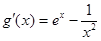 在
在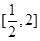 有零点
有零点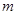
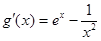 在
在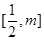 上单调递减,在
上单调递减,在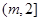 上单调递增……………10分
上单调递增……………10分
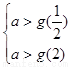 ,即
,即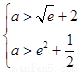 ,
,
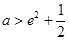 ……………………12分
……………………12分
考点:本题主要考查应用导数研究函数的单调性及极值,简单不等式组的解法。
点评:典型题,本题属于导数应用中的基本问题,对恒成立问题,往往转化成求函数的最值,这种思路是一般解法,通过“分离参数法”,达到解题目的。

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 .
. 时,求
时,求 的单调区间;
的单调区间; 单调增加,在
单调增加,在 单调减少,证明:
单调减少,证明: <6.
<6.
 时,求
时,求 的解集
的解集 的不等式
的不等式 的解集是
的解集是 ,求
,求 的取值范围
的取值范围 .
. 时,求
时,求 的极小值;
的极小值; 对任意的
对任意的 都不是曲线
都不是曲线 的切线,求
的切线,求 的取值范围.
的取值范围.

 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;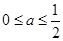 时,讨论
时,讨论 的单调性
的单调性