题目内容
已知p＞0，q＞0，p，q的等差中项是
，x=p+
，y=q+
，则x+y的最小值为（ ）
| 1 |
| 2 |
| 1 |
| p |
| 1 |
| q |
分析：根据等差中项的性质得p+q=1，再把此式和条件代入“x+y”进行整理，根据条件和式子的特点利用基本不等式求出最小值．
解答：解：由题意可得由p，q的等差中项是
得，p+q=1，∵p＞0，q＞0，
∴x+y=p+
+q+
=p+q+
+
=3+
+
≥3+2=5，当且仅当
=
，即p=q=
时，取等号，
故x+y的最小值为5，
故选：C．
| 1 |
| 2 |
∴x+y=p+
| 1 |
| p |
| 1 |
| q |
| p+q |
| p |
| p+q |
| q |
| q |
| p |
| p |
| q |
| p |
| q |
| q |
| p |
| 1 |
| 2 |
故x+y的最小值为5，
故选：C．
点评：本题考查了等差中项的性质和基本不等式求最值的综合应用，关键是化简过程中的“1”代换问题，凑出积为定值，属于中档题．
练习册系列答案
相关题目
，且
，
，求x＋y的最小值．
，且x=p+
，y=q+
，则x+y的最小值是( )
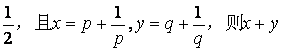的最小值为 .