题目内容
已知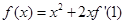 ,则
,则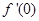 .
.
-4
解析试题分析:∵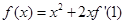 ,两边求导可得
,两边求导可得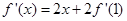 ,令
,令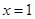 ,得
,得 ,
,
∴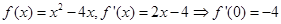 .
.
考点:导数的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
偶函数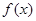 在
在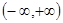 内可导,且
内可导,且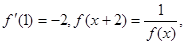 则
则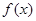 在
在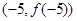 处切线的斜率为( )
处切线的斜率为( )
| A.-2 | B.2 | C.0 | D.无法确定 |
题目内容
已知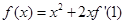 ,则
,则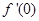 .
.
-4
解析试题分析:∵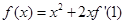 ,两边求导可得
,两边求导可得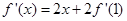 ,令
,令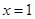 ,得
,得 ,
,
∴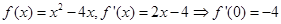 .
.
考点:导数的运用.

 阅读快车系列答案
阅读快车系列答案偶函数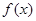 在
在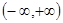 内可导,且
内可导,且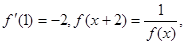 则
则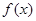 在
在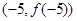 处切线的斜率为( )
处切线的斜率为( )
| A.-2 | B.2 | C.0 | D.无法确定 |