题目内容
在平面直角坐标系中,设点P(X,Y)定义[OP]=|x|+|y|,其中O为坐标原点,对于以下结论:①符合[OP]=1的点P的轨迹围成的图形的面积为2;②设P为直线
| 5 |
③设P为直线y=kx+b(k,b∈R)上的任意一点,则“使[OP]最小的点P有无数个”的必要不充分条件是“k=±1”;其中正确的结论有
分析:①根据新定义由[OP]=|x|+|y|=1,讨论x的取值,得到y与x的分段函数关系式,画出分段函数的图象,由图象可知点P的轨迹围成的图形为边长是
的正方形,求出正方形的面积即可;
②举一个反例,令y=0,求出相应的x,根据新定义求出[OP]=|x|+|y|,即可得到[OP]的最小值为1是假命题;
③根据|x|+|y|大于等于|x+y|或|x-y|,把y=kx+b代入即可得到,当[OP]最小的点P有无数个时,k等于1或-1;而k等于1或-1推出[OP]最小的点P有无数个,所以得到k=±1是“使[OP]最小的点P有无数个”的充要条件,本选项错误.
| 2 |
②举一个反例,令y=0,求出相应的x,根据新定义求出[OP]=|x|+|y|,即可得到[OP]的最小值为1是假命题;
③根据|x|+|y|大于等于|x+y|或|x-y|,把y=kx+b代入即可得到,当[OP]最小的点P有无数个时,k等于1或-1;而k等于1或-1推出[OP]最小的点P有无数个,所以得到k=±1是“使[OP]最小的点P有无数个”的充要条件,本选项错误.
解答:解:①由[OP]=1,根据新定义得:|x|+|y|=1,
可化为:
,
画出图象如图所示:
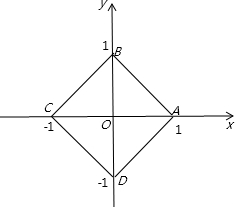
根据图形得到:四边形ABCD为边长是
的正方形,所以面积等于2,本选项正确;
②当P(
,0)时,[OP]=|x|+|y|=
<1,所以[OP]的最小值不为1,本选项错误;
③因为|x|+|y|≥|x+y|=|(k+1)x+b|,当k=-1时,|x|+|y|≥|b|,满足题意;
而|x|+|y|≥|x-y|=|(k-1)x-b|,当k=1时,|x|+|y|≥|b|,满足题意,
所以“使[OP]最小的点P有无数个”的充要条件是“k=±1”,本选项错误.
则正确的结论有:①.
故答案为:①
可化为:
|
画出图象如图所示:

根据图形得到:四边形ABCD为边长是
| 2 |
②当P(
2
| ||
| 5 |
2
| ||
| 5 |
③因为|x|+|y|≥|x+y|=|(k+1)x+b|,当k=-1时,|x|+|y|≥|b|,满足题意;
而|x|+|y|≥|x-y|=|(k-1)x-b|,当k=1时,|x|+|y|≥|b|,满足题意,
所以“使[OP]最小的点P有无数个”的充要条件是“k=±1”,本选项错误.
则正确的结论有:①.
故答案为:①
点评:此题考查学生理解及运用新定义的能力,考查了数形结合的数学思想,是一道中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目