题目内容
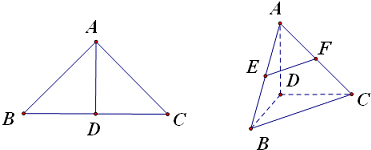 如图,在△ABC中,∠ABC=45°,∠BAC=90°,AD是BC上的高,沿AD把△ABD折起,使∠BDC=90°.
如图,在△ABC中,∠ABC=45°,∠BAC=90°,AD是BC上的高,沿AD把△ABD折起,使∠BDC=90°.(1)若E,F分别为 AB,AC的中点,求证:EF∥平面BDC;
(2)证明:平面ADB⊥平面BDC;
(3 )设BD=1,求三棱锥D-ABC的表面积.
分析:(1)利用三角形中位线定理,可得EF∥BC,结合线面平行的判定定理,可证出EF∥平面BDC;
(2)由CD与AB、AD两条相交直线垂直,得到CD⊥平面ADB,再根据平面ADC经过平面ADB的垂线,可得平面ADB⊥平面BDC;
(3)根据题意不难得到该三棱锥有三个面是全等的等腰直角三角形,另一个面是等边三角形,由此结合BD=1即可得到三棱锥D-ABC的表面积.
(2)由CD与AB、AD两条相交直线垂直,得到CD⊥平面ADB,再根据平面ADC经过平面ADB的垂线,可得平面ADB⊥平面BDC;
(3)根据题意不难得到该三棱锥有三个面是全等的等腰直角三角形,另一个面是等边三角形,由此结合BD=1即可得到三棱锥D-ABC的表面积.
解答:解:(1)在右图中,因为△ABC中,E、F分别为 AB、AC的中点,.
∴EF∥BC
∵EF?平面BDC,BC?平面BDC,
∴EF∥平面BDC;
(2)∵左图中,AD是等腰Rt△ABC斜边BC的中线
∴CD⊥AD,在右图中依然成立
又∵右图中,CD⊥BD,AD、BD是平面ABD内的相交直线
∴CD⊥平面ADB
∵CD?平面BDC,∴平面ADB⊥平面BDC;
(3)由(2)知,AD、BD、CD两两垂直
∵BD=1,∴AD=BD=CD=1
∴三角形ADC的面积S△ADC=
×AD×CD=
,
同理可得S△BDC=S△ABD=
∵Rt△ADC中,AC=
=
,同理可得AB=BC=
∴△ABC是边长为
的等边三角形,面积为S△ABC=
×(
)2=
由此可得三棱锥D-ABC的表面积为:S△ADC+S△BDC+S△ABD+S△ABC=
.

∴EF∥BC
∵EF?平面BDC,BC?平面BDC,
∴EF∥平面BDC;
(2)∵左图中,AD是等腰Rt△ABC斜边BC的中线
∴CD⊥AD,在右图中依然成立
又∵右图中,CD⊥BD,AD、BD是平面ABD内的相交直线
∴CD⊥平面ADB
∵CD?平面BDC,∴平面ADB⊥平面BDC;
(3)由(2)知,AD、BD、CD两两垂直
∵BD=1,∴AD=BD=CD=1
∴三角形ADC的面积S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
同理可得S△BDC=S△ABD=
| 1 |
| 2 |
∵Rt△ADC中,AC=
| AD2+CD2 |
| 2 |
| 2 |
∴△ABC是边长为
| 2 |
| ||
| 4 |
| 2 |
| ||
| 2 |
由此可得三棱锥D-ABC的表面积为:S△ADC+S△BDC+S△ABD+S△ABC=
3+
| ||
| 2 |
点评:本题以等腰直角三角形沿斜边上的高折叠为例,考查了线面平行的判定、面面垂直的判定和几何体的表面积求法等知识点,属于基础题.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,
如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm, 如图,在△ABC中,设
如图,在△ABC中,设 如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.
如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3. 如图,在△ABC中,已知
如图,在△ABC中,已知