题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
解:当n=1时,a1=S1=2 当n>1时,an=Sn-Sn-1=n+1, 综上,数列{an}的通项公式是an=n+1( |
(2) |
解:bn=12´
32-(n+1)=36´
b1=12, ∴Tn= 由此可知12≤Tn<18 而{Sn}是一个递增数列, 且S1=2,T1=12,S2=5,T2=16,S3=9,T3= 故存在一个最小正整数M=4,当n>M时,Sn>Tn恒成立.(12分) |

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
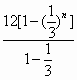 =18(1-
=18(1-