题目内容
(本小题满分12分)
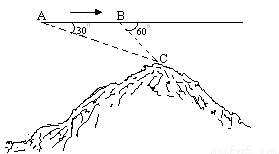
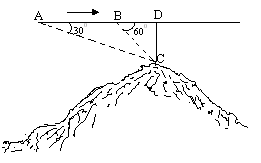
如图,飞机的航线和山顶在同一个铅直平面内,已知飞机的高度为海拔25000米,速度为3000米/分钟,飞行员先在点A看到山顶C的俯角为300,经过8分钟后到达点B,此时看到山顶C的俯角为600,则山顶的海拔高度为多少米.(参考数据: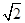 =1.414,
=1.414,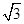 =1.732,
=1.732,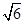 =2.449).
=2.449).
【答案】
4216
【解析】
试题分析:如图,过C作AB的垂线,垂足为D,
 依题意,AB=3000·8=24000米,
依题意,AB=3000·8=24000米,
由∠BAC=300,∠DBC=600,则∠BCA=300,∴ BC=24000米, 在直角三角形CBD中,
CD=BC· =24000·0.866=20784米,
=24000·0.866=20784米,
故山顶的海拔高度为25000-20784=4216米.
考点:本题考查了正余弦定理的实际运用
点评:正余弦定理在测量、航海、物理、几何、天体运行等方面的应用十分广泛,解这类应用题需要我们吃透题意,对专业名词、术语要能正确理解,能将实际问题归结为数学问题.求解此类问题的大概步骤为:(1)准确理解题意,分清已知与所求,准确理解应用题中的有关名称、术语,如仰角、俯角、视角、象限角、方位角等;(2)根据题意画出图形;(3)将要求解的问题归结到一个或几个三角形中,通过合理运用正弦定理、余弦定理等有关知识建立数学模型,然后正确求解,演算过程要简练,计算要准确,最后作答

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目