Question

如图，在△ABC中，∠B=

π

2

，AB=BC=2，P为AB边上一动点，PD∥BC，P为AB边上一动点，PD∥BC交AC于点D，现将△PDA沿PD翻折至△PDA′，使平面PDA′⊥平面PBCD．
（1）当棱锥A′-PBCD的体积最大时，求PA的长；
（2）若点P为AB的中点，E为A′C的中点，求证：A′B⊥DE．

Answer 1

分析：（1）令PA=x（0＜x＜2）求出体积表达式，利用导数确定函数的单调性，求出函数的最大值．
（2）设F为A′B的中点，连接PF，FE，通过PDEF是平行四边形，证明A′B⊥DE．

解答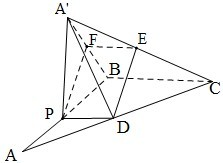：解：（1）令PA=x（0＜x＜2），则A′P=PD=x．BP=2-x，因为A′P⊥PD
且平面A′PD⊥平面PBCD，故A′P⊥平面PBCD，所以VA′-PBCD=

1

3

Sh=

1

6

(2-x)(2+x)x=

1

6

(4x-x3)
令f（x）=

1

6

(4x-x3)，由f′（x）=

1

6

(4-3x2) =0得x=

2 3

3

，
当x∈（0，

2 3

3

）时，f′（x）＞0，f（x）单调递增，
当x∈（

2 3

3

，2）时，f′（x）＜0，f（x）单调递减，
所以，当x=

2 3

3

时，f（x）取得最大值，
即：体积最大时，PA=

2 3

3

．
（2）设F为A′B的中点，连接PF，FE，则有EF∥BC，EF=

1

2

BC，PD∥BC，PD=

1

2

BC，
所以DE∥PF，又A′P=PB，所以PF⊥A′B．
故DE⊥A′B

点评：本题是中档题，考查几何体的体积计算，函数最大值的求法，直线与直线的垂直的证明方法，考查空间想象能力，计算能力．