题目内容
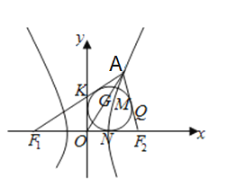
【题目】在双曲线![]() 的右支上存在点
的右支上存在点![]() ,使得点
,使得点![]() 与双曲线的左、右焦点
与双曲线的左、右焦点![]() ,
,![]() 形成的三角形的内切圆
形成的三角形的内切圆![]() 的半径为
的半径为![]() ,若
,若![]() 的重心
的重心![]() 满足
满足![]() ,则双曲线
,则双曲线![]() 的离心率为__________.
的离心率为__________.
【答案】2
【解析】
设![]() ,
,![]() ,
,![]() ,运用三角形的重心坐标,求得内心的坐标,可得
,运用三角形的重心坐标,求得内心的坐标,可得![]() ,再结合双曲线的定义和等积法,求得
,再结合双曲线的定义和等积法,求得![]() ,再由双曲线的离心率公式和第二定义,可得
,再由双曲线的离心率公式和第二定义,可得![]() ,将
,将![]() 的坐标代入双曲线的方程,运用
的坐标代入双曲线的方程,运用![]() ,
,![]() ,
,![]() 的关系和离心率公式,即可得到所求离心率.
的关系和离心率公式,即可得到所求离心率.
设![]() ,
,![]() ,
,![]() ,
,
可得重心![]() ,即
,即![]() ,
,
设△![]() 的内切圆与边
的内切圆与边![]() 的切点
的切点![]() ,与边
,与边![]() 的切点为
的切点为![]() ,与边
,与边![]() 上的切点为
上的切点为![]() ,
,
则△![]() 的内切圆的圆心的横坐标与
的内切圆的圆心的横坐标与![]() 的横坐标相同.
的横坐标相同.
由双曲线的定义,![]() .①
.①
由圆的切线性质![]() ,
,
![]() ,
,![]() ,
,![]() ,即有
,即有![]() 。
。
由![]() ,
,
则△![]() 的重心为
的重心为![]() ,
,![]() ,即
,即![]() ,
,
由△![]() 的面积为
的面积为![]() ,
,
可得![]() .②
.②
由①②可得![]() ,
,
由右准线方程![]() ,双曲线的第二定义可得:
,双曲线的第二定义可得:
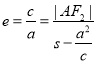 ,解得
,解得![]() ,
,
即有![]() ,代入双曲线的方程可得
,代入双曲线的方程可得![]() ,可得
,可得![]() ,
,
可得双曲线的离心率为![]() .
.
故答案为:![]() .
.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目