题目内容
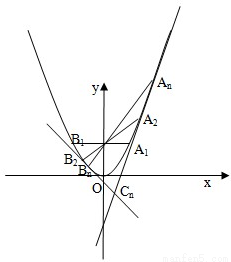
如图，对每个正整数n，An(xn，yn)是抛物线x2＝4y上的点，过焦点F的直线FAn交抛物线于另一点Bn(Sn，tn)．Cn为抛物线上分别以An与Bn为切点的两条切线的交点．
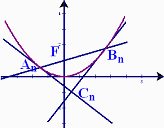
(1)求证∠AnCnBn＝90o；
(2)求证点Cn的纵坐标是一个定值，并求这个定值；
(3)若|FC1|、|FC2|、|FC3|、…、|FCn|构成首项为3，公比为2的等比数列，求|A1B1|＋|A2B2|＋|A3B3|＋…＋|AnBn|．
答案：
解析：
解析：
|
证明：(1)对任意固定的 由一元二次方程根与系数的关系得 对任意固定的 故 类似地，可求得 又 (2)又由②－①得： 将③代入①并注意 (3)由抛物线定义知， 故 而由两点间的距离公式得： 故 故 所以 |
因为焦点F(0，1)，所以可设直线
的方程为
将它与抛物线方程
联立得
，
……★
处的切线的斜率
，……①
处的切线的方程为：
，……②
故∠AnCnBn＝90o
，
……③
得交点
的纵坐标为－1．
，
，又
，
＝
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
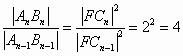
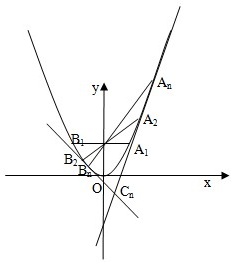如图，对每个正整数n，An（xn，yn）是抛物线x2=4y上的点，过焦点F的直线FAn交抛物线于另一点Bn（sn，tn）．
