题目内容
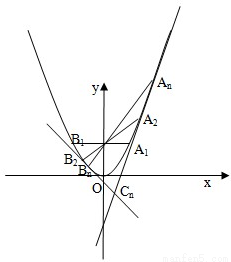
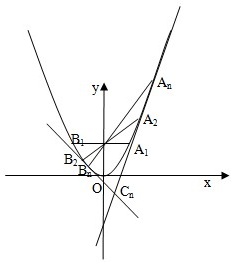 如图,对每个正整数n,An(xn,yn)是抛物线x2=4y上的点,过焦点F的直线FAn交抛物线于另一点Bn(sn,tn).
如图,对每个正整数n,An(xn,yn)是抛物线x2=4y上的点,过焦点F的直线FAn交抛物线于另一点Bn(sn,tn).(Ⅰ)试证:xnsn=-4(n≥1);
(Ⅱ)取xn=2n,并记Cn为抛物线上分别以An与Bn为切点的两条切线的交点.试证:|FC1|+|FC2|+…+|FCn|=2n-2-n+1+1.
分析:(Ⅰ)先设直线AnBn的方程为y-1=knx,然后与抛物线方程x2=4y联立消去y得到x2-4knx-4=0,再由根与系数的关系可得到xnsn=-4,从而得证.
(Ⅱ)先根据导数求出抛物线x2=4y在An处的切线的斜率,进而可得到抛物线在An处的切线的方程,同理可得到x2=4y在Bn处的切线方程,然后两切线方程相减整理可得到交点Cn的坐标,然后结合两点间的距离公式可得到|FCn|2=(
)2+4=
+
+2整理即可得到|FCn|=
+
,又由于xn=2n可得到|FC1|+|FC2|+…+|FCn|=
(|x1|+|x2|+…+|xn|)+2(
+
+…+
)=
(2+22+…+2n)+2(
+
+…+
),最后根据等比数列的前n项和公式可得到最后答案.
(Ⅱ)先根据导数求出抛物线x2=4y在An处的切线的斜率,进而可得到抛物线在An处的切线的方程,同理可得到x2=4y在Bn处的切线方程,然后两切线方程相减整理可得到交点Cn的坐标,然后结合两点间的距离公式可得到|FCn|2=(
| xn+sn |
| 2 |
| ||
| 4 |
| ||
| 4 |
| |xn| |
| 2 |
| 2 |
| |xn| |
| 1 |
| 2 |
| 1 |
| |x1| |
| 1 |
| |x2| |
| 1 |
| |xn| |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
解答:证明:(Ⅰ)对任意固定的n≥1,因为焦点F(0,1),
所以可设直线AnBn的方程为y-1=knx,
将它与抛物线方程x2=4y联立得:x2-4knx-4=0,
由一元二次方程根与系数的关系得xnsn=-4(n≥1).
(Ⅱ)对任意固定的n≥1,
利用导数知识易得抛物线x2=4y在An处
的切线的斜率kAn=
,
故x2=4y在An处的切线的方程为:y-yn=
(x-xn),①
类似地,可求得x2=4y在Bn处的切线的方程为:y-tn=
(x-sn),②
由②-①得:yn-tn=-
x+
=
-
,
x=
,∴x=
③
将 ③代入 ①并注意xnsn=-4得交点Cn的坐标为(
,-1).
由两点间的距离公式得:|FCn|2=(
)2+4=
+
+2=
+
+2=(
+
)2,?|FCn|=
+
.
现在xn=2n,利用上述已证结论并由等比数列求和公式得:
|FC1|+|FC2|+…+|FCn|=
(|x1|+|x2|+…+|xn|)+2(
+
+…+
)
=
(2+22+…+2n)+2(
+
+…+
)=(2n-1)+(2-21-n)=2n-2-n+1+1.
所以可设直线AnBn的方程为y-1=knx,
将它与抛物线方程x2=4y联立得:x2-4knx-4=0,
由一元二次方程根与系数的关系得xnsn=-4(n≥1).
(Ⅱ)对任意固定的n≥1,
利用导数知识易得抛物线x2=4y在An处
的切线的斜率kAn=
| xn |
| 2 |
故x2=4y在An处的切线的方程为:y-yn=
| xn |
| 2 |
类似地,可求得x2=4y在Bn处的切线的方程为:y-tn=
| sn |
| 2 |
由②-①得:yn-tn=-
| xn-sn |
| 2 |
| ||||
| 2 |
| ||
| 4 |
| ||
| 4 |
| xn-sn |
| 2 |
| ||||
| 4 |
| xn+sn |
| 2 |
将 ③代入 ①并注意xnsn=-4得交点Cn的坐标为(
| xn+sn |
| 2 |
由两点间的距离公式得:|FCn|2=(
| xn+sn |
| 2 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| 4 | ||
|
| xn |
| 2 |
| 2 |
| xn |
| |xn| |
| 2 |
| 2 |
| |xn| |
现在xn=2n,利用上述已证结论并由等比数列求和公式得:
|FC1|+|FC2|+…+|FCn|=
| 1 |
| 2 |
| 1 |
| |x1| |
| 1 |
| |x2| |
| 1 |
| |xn| |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
点评:本题主要考查直线与抛物线的综合问题和等比数列的前n项和公式.考查基础知识的综合运用和计算能力.圆锥曲线、直线以及数列是高考必考题,要给予重视.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目