题目内容
(22)如图,对每个正整数n,An(xn,yn)是抛物线x2=4y上的点,过焦点F的直线FA.交抛物线于另一点Bn(sn,tn).
(Ⅰ)试证:xnsn=-4(n≥1);
(Ⅱ)取xn=2n,并记Cn为抛物线上分别以An与Bn为切点的两条切线的交点.试证:
|FC1|+|FC2|+…+|FCn|=2n-2-n+1+1(n≥1).
证明:(Ⅰ)对任意固定的n≥1,因为焦点F(0,1),所以可设直线AnBn的方程为y-1=knx,将它与抛物线x2=4y联立得
x2-4knx-4=0.
由一元二次方程根与系数的关系得xnsn=-4.
(Ⅱ)对任意固定的n≥1,利用导数知识易得抛物线x2=4y在An处的切线的斜率![]() =
=![]()
故x2=4y在An处切线方程为
y-yn=![]() (x-xn), ①
(x-xn), ①
类似地,可求得x2=4y在Bn处的切线方程为
y-tn=![]() (x-sn). ②
(x-sn). ②
由②减去①得
yn-tn=-![]()
从而 ![]()
![]()
![]() ③
③
将③代入①并注意xnsn=-4得交点Cn的坐标为(![]() ,-1).
,-1).
由两点间的距离公式得
|FCn|2=![]()
=![]()
从而 |FCn|-![]()
现在xn=2n.利用上述已证结论并由等比数列求和公式得,
|FC1|+|FC2|+…+|FCn|
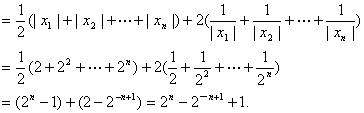

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
一般来说,一个人脚掌越长,他的身高就越高,现对10名成年人的脚掌长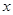 与身高
与身高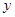 进行测量,得到数据(单位均为
进行测量,得到数据(单位均为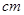 )如表,作出散点图后,发现散点在一条直线附近,经计算得到一些数据:
)如表,作出散点图后,发现散点在一条直线附近,经计算得到一些数据: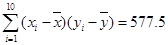 ,
,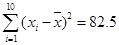 ;某刑侦人员在某案发现场发现一对裸脚印,量得每个脚印长为
;某刑侦人员在某案发现场发现一对裸脚印,量得每个脚印长为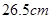 ,则估计案发嫌疑人的身高为
,则估计案发嫌疑人的身高为
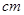 .
.
|
脚长 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
|
身高 |
141 |
146 |
154 |
160 |
169 |
176 |
181 |
188 |
197 |
203 |
 11、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.
11、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.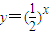 的图象上,且数列{an} 是a1=1,公差为d的等差数列.
的图象上,且数列{an} 是a1=1,公差为d的等差数列.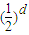 的等比数列;
的等比数列;