题目内容
17.关于x的方程$\sqrt{1{-x}^{2}}$=mx+1(m∈R)有一个实根时,m的取值范围为(-∞,-1)∪(1,+∞)∪{0}.分析 作出函数y=$\sqrt{1-{x}^{2}}$和y=mx+1的图象,由题意可得只要考虑直线与半圆有一个交点的情况.
解答 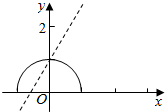 解:作出函数y=$\sqrt{1-{x}^{2}}$和y=mx+1的图象,
解:作出函数y=$\sqrt{1-{x}^{2}}$和y=mx+1的图象,
y=$\sqrt{1-{x}^{2}}$为上半圆,y=mx+1为恒过定点(0,1)的直线,
当m=0时,y=1显然和半圆相切,有一个交点;
当直线y=mx+1过(-1,0)和(1,0)时,m=1,-1.
由图象可得当m>1或m<-1时,有一个交点.
则方程有一个实根时,m的范围是(-∞,-1)∪(1,+∞)∪{0}.
故答案为:(-∞,-1)∪(1,+∞)∪{0}.
点评 本题考查函数和方程的转化思想,考查数形结合的思想方法,作出函数的图象是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.设a>b>0,a+b=1,且x=logab,y=log${\;}_{\frac{1}{b}}$a,z=log${\;}_{(\frac{1}{a}+\frac{1}{b})}$(3a+b).则x,y,z之间的大小关系是( )
| A. | y<x<z | B. | z<y<x | C. | x<y<z | D. | y<z<x |
6.在等差数列{an}中,若a1=2,a3=8,则a2等于( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |