Question

函数f(x)=

1

2

(sinx+cosx)-

1

2

|sinx-cosx|-m，x∈[0，2π]，若f（x）=0有四个不同的实根，则m的取值范围是（　　）

• A、(-

  2

  2

  ，

  2

  2

  )
• B、(-1，-

  2

  2

  )
• C、（-1，1）
• D、(-

  2

  2

  ，1)

Answer 1

分析：若f（x）=0有四个不同的实根，可转化成y=m与y=

1

2

（sinx+cosx）-

1

2

|sinx-cosx|，在x∈[0，2π]上有四个交点，去掉绝对值，画出图象，观察图形即可求出m的范围．

解答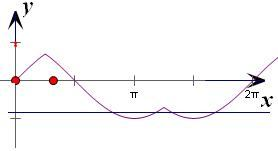：解：可转化成y=m与y=

1

2

（sinx+cosx）-

1

2

|sinx-cosx|，
在x∈[0，2π]上有四个交点
当sinx≥cosx时，即x∈[

π

4

，

5π

4

]此时y=cosx
当sinx＜cosx时，此时y=sinx
结合图象可知，m∈(-1，-

2

2

)
故选B

点评：本题主要考查了函数与方程的综合运用，以及正余弦函数的图象和去绝对值的方法，属于基础题．