Question

已知点P（x，y）满足

(x-1)2+(y-2)2

-

(x-4)2+(y-6)2

=5，则

y-2

x+4

的取值范围是

[

1

2

，+∞）

．

Answer 1

分析：利用双曲线的定义可得其点P的轨迹是双曲线的一支，再利用斜率的几何意义即可得出．

解答：解：由两点间的距离公式

(x-1)2+(y-2)2

表示两点P（x，y）与F₁（1，2）之间的距离，同理

(x-4)2+(y-6)2

表示两点P（x，y）与F₂（4，6）之间的距离．
由条件点P满足

(x-1)2+(y-2)2

-

(x-4)2+(y-6)2

=5，如图所示．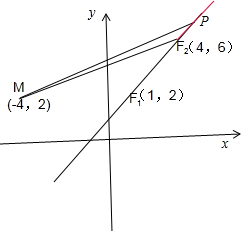
可知：而|F1F2|=

32+42

=5．
∴点P（x，y）是到两定点F₁（1，2），F₂（4，6）的距离的差等于5一条射线．
而

y-2

x+4

表示过两点P（x，y），（-4，2）的斜率．
令k=

y-2

x+4

，则k≥kMF2=

6-2

4-(-4)

=

1

2

．
∴

y-2

x+4

的取值范围是[

1

2

，+∞）．
故答案为[

1

2

，+∞）．

点评：数列掌握双曲线的定义和斜率的计算公式是解题的关键．