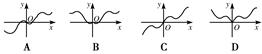题目内容
设函数f(x)=g(x)+x2,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则曲线y=f(x)在点(1,f(1))处的切线的斜率为( )
| A.2 | B.- | C.4 | D.- |
C
解析

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
函数y=f(x)在定义域(-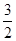 ,3)内的图像如图所示.记y=f(x)的导函数为y=f¢(x),则不等式f¢(x)≤0的解集为( )
,3)内的图像如图所示.记y=f(x)的导函数为y=f¢(x),则不等式f¢(x)≤0的解集为( )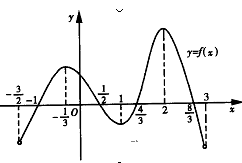
A.[-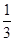 ,1]∪[2,3) ,1]∪[2,3) |
B.[-1, ]∪[ ]∪[ , , ] ] |
C.[-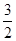 , , ]∪[1,2) ]∪[1,2) |
D.(-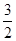 ,- ,-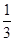 ]∪[ ]∪[ , , ]∪[ ]∪[ ,3) ,3) |
方程 的实根个数是( )
的实根个数是( )
| A.3 | B.2 | C.1 | D.0 |
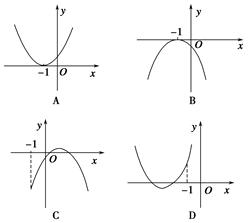
已知e为自然对数的底数,则函数y=xex的单调递增区间是( )
| A.[-1,+∞) | B.(-∞,-1] |
| C.[1,+∞) | D.(-∞,1] |
曲线y=sinx,y=cosx与直线x=0,x=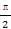 所围成的平面区域的面积为( )
所围成的平面区域的面积为( )
A.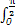 (sinx-cosx)dx (sinx-cosx)dx | B.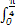 (sinx-cosx)dx (sinx-cosx)dx |
C.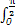 (cosx-sinx)dx (cosx-sinx)dx | D.2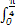 (cosx-sinx)dx (cosx-sinx)dx |
函数f(x)=3x2+ln x-2x的极值点的个数是( )
| A.0 | B.1 |
| C.2 | D.无数个 |
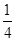 x2+
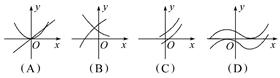
x2+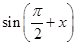 ,f′(x)为f(x)的导函数,则f′(x)的图象是( )
,f′(x)为f(x)的导函数,则f′(x)的图象是( )