题目内容
13.已知函数f(x)=log2$\frac{x}{1-x}$+1,an=f($\frac{1}{n}$)+f($\frac{2}{n}$)+…+f($\frac{n-1}{n}$),n为正整数,则a2015=2014.分析 构造函数f(x)=log2$\frac{x}{1-x}$+1,由f(x)+f(1-x)=2结合已知利用倒序相加法得答案.
解答 解:∵f(x)=log2$\frac{x}{1-x}$+1,
∴$f(1-x)=lo{g}_{2}\frac{1-x}{1-(1-x)}+1$=$lo{g}_{2}\frac{1-x}{x}+1$,
∴f(x)+f(1-x)=2,
又∵an=f($\frac{1}{n}$)+f($\frac{2}{n}$)+…+f($\frac{n-1}{n}$),
∴a2015=f($\frac{1}{2015}$)+f($\frac{2}{2015}$)+…+f($\frac{2014}{2015}$)
a2015=f($\frac{2014}{2015}$)+f($\frac{2013}{2015}$)…+f($\frac{1}{2015}$)
将上述两式相加得2a2015=2×2014
∴a2015=2014
故答案为:2014.
点评 本题考查了对数的运算性质,考查了函数构造法,是中档题.

练习册系列答案
相关题目
18.在△ABC 中,若A=$\frac{π}{3}$,cosB=$\frac{{\sqrt{6}}}{3}$,BC=6,则 AC=( )
| A. | 4$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |
 已知函数f(x)=x2-ax的图象在点A(1,f(1))处的切线与直线x+3y+2=0垂直,执行如图所示的程序框图,输出的k值是6.
已知函数f(x)=x2-ax的图象在点A(1,f(1))处的切线与直线x+3y+2=0垂直,执行如图所示的程序框图,输出的k值是6.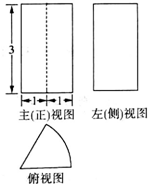 某圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为$\frac{π}{3}$的扇形,则该几何体的体积为2π.
某圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为$\frac{π}{3}$的扇形,则该几何体的体积为2π.