题目内容
8.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别是点F1,F2,其离心率e=$\frac{1}{2}$,点P为椭圆上的一个动点,△PF1F2面积的最大值为4$\sqrt{3}$.(Ⅰ)求椭圆的方程;
(Ⅱ)若A,B,C,D是椭圆上不重合的四个点,AC与BD相交于点F1,$\overrightarrow{AC}$$•\overrightarrow{BD}$=0,求|$\overrightarrow{AC}$|+|$\overrightarrow{BD}$|的取值范围.
分析 (Ⅰ)容易知道当P点为椭圆的上下顶点时,△PF1F2面积最大,再根据 椭圆的离心率为$\frac{1}{2}$可得到关于a,c的方程组$\left\{\begin{array}{l}{\sqrt{{a}^{2}-{c}^{2}}c=4\sqrt{3}}\\{\frac{c}{a}=\frac{1}{2}}\end{array}\right.$,解该方程组即可得到a,c,b,从而得出椭圆的方程$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$;
(Ⅱ)先容易求出AC,BD中有一条直线不存在斜率时|$\overrightarrow{AC}$|+|$\overrightarrow{BD}$|=14,当直线AC存在斜率k且不为0时,写出直线AC的方程y=k(x+2),联立椭圆的方程消去y得到(3+4k2)x2+16k2x+16k2-48=0,根据韦达定理及弦长公式即可求得$|\overrightarrow{AC}|=\frac{24({k}^{2}+1)}{3+4{k}^{2}}$,把k换上$-\frac{1}{k}$即可得到$|\overrightarrow{BD}|=\frac{24({k}^{2}+1)}{4+3{k}^{2}}$.所以用k表示出$|\overrightarrow{AC}|+|\overrightarrow{BD}|=\frac{168({k}^{2}+1)}{(3+4{k}^{2})(4+3{k}^{2})}$,这时候设k2+1=t,t>1,从而得到$|\overrightarrow{AC}|+|\overrightarrow{BD}|=\frac{168}{12+\frac{t-1}{{t}^{2}}}$,根据导数求出$\frac{t-1}{{t}^{2}}$的范围,从而求出$|\overrightarrow{AC}|+|\overrightarrow{BD}|$的取值范围.
解答 解:(Ⅰ)由题意知,当P是椭圆的上下顶点时△PF1F2的面积取最大值;
∴$\frac{1}{2}•2c•b=4\sqrt{3}$;
即$\sqrt{{a}^{2}-{c}^{2}}c=4\sqrt{3}$①;
由离心率为$e=\frac{1}{2}$得:
$\frac{c}{a}=\frac{1}{2}$②;
∴联立①②解得a=4,c=2,b2=12;
∴椭圆的方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$;
(Ⅱ)由(Ⅰ)知F1(-2,0);
∵$\overrightarrow{AC}•\overrightarrow{BD}=0$,∴AC⊥BD;
(1)当直线AC,BD中一条直线斜率不存在时,$|\overrightarrow{AC}|+|\overrightarrow{BD}|=8+6=14$;
(2)当直线AC斜率为k,k≠0时,其方程为y=k(x+2),将该方程带入椭圆方程并整理得:
(3+4k2)x2+16k2x+16k2-48=0;
若设A(x1,y1),B(x2,y2),则:${x}_{1}+{x}_{2}=\frac{-16{k}^{2}}{3+4{k}^{2}},{x}_{1}{x}_{2}=\frac{16{k}^{2}-48}{3+4{k}^{2}}$;
∴$|\overrightarrow{AC}|=\sqrt{1+{k}^{2}}\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{24({k}^{2}+1)}{3+4{k}^{2}}$;
直线BD的方程为y=$-\frac{1}{k}(x+2)$,同理可得$|\overrightarrow{BD}|=\frac{24({k}^{2}+1)}{4+3{k}^{2}}$;
∴$|\overrightarrow{AC}|+|\overrightarrow{BD}|$=$\frac{168({k}^{2}+1)^{2}}{(3+4{k}^{2})(4+3{k}^{2})}$;
令k2+1=t,t>1;
∴$|\overrightarrow{AC}|+|\overrightarrow{BD}|=\frac{168{t}^{2}}{(4t-1)(3t+1)}$=$\frac{168{t}^{2}}{12{t}^{2}+t-1}$=$\frac{168}{12+\frac{t-1}{{t}^{2}}}$;
设f(t)=$\frac{t-1}{{t}^{2}}$,(t>1),f′(t)=$\frac{-t+2}{{t}^{3}}$;
∴t∈(1,2)时,f′(t)>0,t∈(2,+∞)时,f′(t)<0;
∴t=2时,f(t)取最大值$\frac{1}{4}$,又f(t)>0;
∴$0<\frac{t-1}{{t}^{2}}≤\frac{1}{4}$;
∴$|\overrightarrow{AC}|+|\overrightarrow{BD}|$$∈[\frac{96}{7},14)$;
∴综上得$|\overrightarrow{AC}|+|\overrightarrow{BD}|$的取值范围为$[\frac{96}{7},14]$.
点评 考查三角形的面积公式,椭圆离心率的概念,椭圆的标准方程,a,b,c三个系数的几何意义,直线的点斜式方程,以及弦长公式,根据导数求函数最值的方法.

| A. | -2i | B. | 2i | C. | -4i | D. | 4i |
| A. | -2-i | B. | 2-i | C. | 2+i | D. | -2+i |
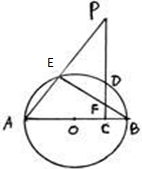 如图AB为圆O直径,P为圆O外一点,过P点作PC⊥AB,垂足为C,PC交圆O于D点,PA交圆O于E点,BE交PC于F点
如图AB为圆O直径,P为圆O外一点,过P点作PC⊥AB,垂足为C,PC交圆O于D点,PA交圆O于E点,BE交PC于F点 某商场每天上午10 点开门,晚上 19 点停止进入.在如图所示的框图中,t表示整点时刻,a(t )表示时间段[t-1,t)内进入商场人次,S 表示某天某整点时刻前进入商场人次总和,为了统计某天进入商场的总人次数,则判断框内可以填( )
某商场每天上午10 点开门,晚上 19 点停止进入.在如图所示的框图中,t表示整点时刻,a(t )表示时间段[t-1,t)内进入商场人次,S 表示某天某整点时刻前进入商场人次总和,为了统计某天进入商场的总人次数,则判断框内可以填( )