题目内容
对大于或等于2的自然数m的n次方幂有如下分解式：
22=1+3 32=1+3+5 42=1+3+5+7 …
23=3+5 33=7+9+11 …
24=7+9 …
按此规律，54的分解式中的第三个数为________．
29
分析：由题意知，n的三次方就是n个连续奇数相加，且从2开始，这些4次方的分解正好是从奇数7开始连续出现，由此规律即可建立m4（m∈N*）的分解方法．
解答：由题意，从23到m3，正好用去从3开始的连续奇数共2+3+4+…+m=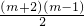
个，
即从24到44，用去从7开始的连续奇数共
=9个
故54的分解式中第一个奇数为25，且共有5个连续奇数相加，
故54=25+27+29+31+33．
故答案为：29．
点评：本题考查归纳推理，求解的关键是根据归纳推理的原理归纳出结论，其中分析出分解式中项数及每个式子中各数据之间的变化规律是解答的关键．
分析：由题意知，n的三次方就是n个连续奇数相加，且从2开始，这些4次方的分解正好是从奇数7开始连续出现，由此规律即可建立m4（m∈N*）的分解方法．
解答：由题意，从23到m3，正好用去从3开始的连续奇数共2+3+4+…+m=
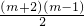个，即从24到44，用去从7开始的连续奇数共
=9个故54的分解式中第一个奇数为25，且共有5个连续奇数相加，
故54=25+27+29+31+33．
故答案为：29．
点评：本题考查归纳推理，求解的关键是根据归纳推理的原理归纳出结论，其中分析出分解式中项数及每个式子中各数据之间的变化规律是解答的关键．
练习册系列答案
名校课堂系列答案
相关题目
