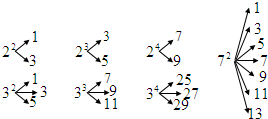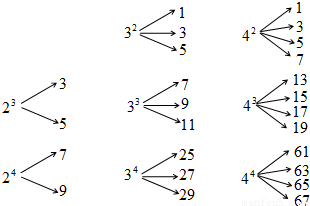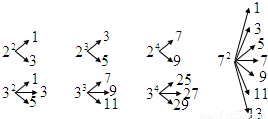Question

如图，对大于或等于2的自然数m的n次幂进行如下方式的“分裂”：

仿此，6²的“分裂”中最大的数是

11

；2013³的“分裂”中最大的数是

2013²+2012

．

Answer 1

分析：根据所给的数据，不难发现：在n²中所分解的最大的数是2n-1；在m³中，所分解的最大数是m²+m-1．根据发现的规律可求．

解答：解：对大于或等于2的自然数m的n次幂进行如下方式的“分裂”，不难发现：在n²中所分解的最大的数是2n-1；
故6²的“分裂”中最大的数是11（本空2分）；
在m³（m为奇数）的“分拆”的最大数是m²+m-1，
所以2013²+2012=4054181（本空（3分），写成“2013²+2012”或“4054181”都给3分）
故答案为：11；2013²+2012．

点评：此题首先要根据所提供的数据具体发现规律，然后根据发现的规律求解．规律为：在n²中所分解的最大的数是2n-1；在n³中，所分解的最小数是n²-n+1