题目内容
17.已知x1,x2为方程x2-2x+a=0的两根,f(x)=$\frac{1}{3}$x3-x2+ax-a,若f(x1)f(x2)>0,求实数a的取值范围.分析 分△=0与△>0讨论,当△>0时,利用x1+x2=2,x1x2=a,x12-2x1+a=0,x22-2x2+a=0化简f(x1)f(x2)>0可得a(a2-3a+3)>0,从而解得.
解答 解:(1)当△=4-4a=0,即a=1时,
x1=x2=1,f(x1)f(x2)=$(-\frac{2}{3})^{2}$>0,符合题意;
(2)当△=4-4a>0,即a<1时,
x1+x2=2,x1x2=a,x12-2x1+a=0,x22-2x2+a=0;
∴f(x1)=$\frac{1}{3}$x13-x12+ax1-a
=$\frac{1}{3}$x1(2x1-a)-(2x1-a)+ax1-a
=$\frac{2}{3}$x12-$\frac{1}{3}$ax1-2x1+a+ax1-a
=$\frac{2}{3}$(2x1-a)-$\frac{1}{3}$ax1-2x1+ax1
=$\frac{2}{3}$(a-1)x1-$\frac{2}{3}$a,
同理,f(x2)=$\frac{2}{3}$(a-1)x2-$\frac{2}{3}$a,
∴f(x1)f(x2)=[$\frac{2}{3}$(a-1)x1-$\frac{2}{3}$a][$\frac{2}{3}$(a-1)x2-$\frac{2}{3}$a]
=$\frac{4}{9}$((a-1)2x1x2-a(a-1)(x1+x2)+a2)
=$\frac{4}{9}$(a(a-1)2-2a(a-1)+a2)>0,
即a(a2-3a+3)>0,
∴a>0,
又∵a<1,
∴0<a<1;
故实数a的取值范围为(0,1].
点评 本题考查了分类讨论的思想应用及方程的根与系数的关系应用.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
7.函数y=sinx的图象( )
| A. | 关于点$({\frac{π}{2},1})$对称 | B. | 关于直线x=π对称 | C. | 关于点(π,0)对称 | D. | 关于y轴对称 |
5.函数f(x)=ex+lnx在点(1,f(1))处的切线的斜率为( )
| A. | e | B. | e+1 | C. | -1 | D. | 2e |
12.已知p:|x-3|≤2,q:(x-m+1)(x-m-1)≤0,若p是q的必要不充分条件,则实数m的取值范围是( )
| A. | 2≤m≤4 | B. | R | C. | 2<m<4 | D. | m>4或m<2 |
6.函数f(x)=$\left\{\begin{array}{l}{\frac{ln(x+1)}{x-1}\\;x>1}\\{tan\frac{π}{2}x\\;0≤x<1}\\{x+sinx\\;x<0}\end{array}\right.$的全体连续点的集合是( )
| A. | (-∞,+∞) | B. | (-∞,0)∪(0,+∞) | C. | (-∞,1)∪(1,+∞) | D. | (-∞,0)∪(0,1)∪(1,+∞) |
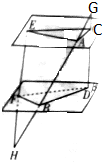 如图,已知α∥β,GH、GD、HE分别交α、β于A、B、C、D、E、F且GA=9,AB=12,BH=16,S△AEC=72,求S△BFD.
如图,已知α∥β,GH、GD、HE分别交α、β于A、B、C、D、E、F且GA=9,AB=12,BH=16,S△AEC=72,求S△BFD.