题目内容
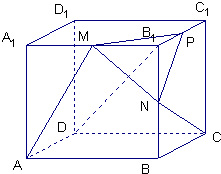 在棱长为2的正方体ABCD-A1B1C1D1中,M、N分别是A1B1和B1B的中点.
在棱长为2的正方体ABCD-A1B1C1D1中,M、N分别是A1B1和B1B的中点.(1)求直线AM和CN所成角的大小;
(2)若P为B1C1的中点,求证:B1D⊥平面PMN;
(3)求点A到平面PMN的距离.
分析:(1)先通过平移将两条异面直线平移到同一个起点B1,得到的锐角或直角就是异面直线所成的角,在三角形中再利用余弦定理求出此角即可;
(2)根据面面平行的判定定理证明平面A1C1B∥平面MNP,而B1D⊥平面A1C1B,从而得到结论;
(3)利用等体积转化,设点A到平面PMN的距离为h,VA-MNP=VP-MNA建立等式,解之即可求出所求.
(2)根据面面平行的判定定理证明平面A1C1B∥平面MNP,而B1D⊥平面A1C1B,从而得到结论;
(3)利用等体积转化,设点A到平面PMN的距离为h,VA-MNP=VP-MNA建立等式,解之即可求出所求.
解答:解:(1)如图,将AM平移到B1E,NC平移到B1F,则∠EB1F为直线AM与CN所成角或其补角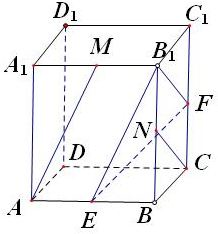
设边长为2,则B1E=B1F=
,EF=
∴由余弦定理得cos∠EB1F=
,
即直线AM和CN所成角的大小为arccos
(2)根据中位线定理可知MN∥A1B,NP∥C1B
∴MN∥平面A1C1B,NP∥平面A1C1B,MN∩NP=P
∴平面A1C1B∥平面MNP,
而B1D⊥平面A1C1B,
所以B1D⊥面PMN;
(3)S△MNP=
,S△MNA=
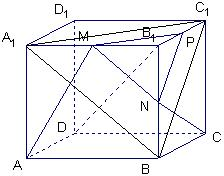
设点A到平面PMN的距离为h
∴VA-MNP=VP-MNA
即
S△MNPh=
S△MNA×1
∴h=

设边长为2,则B1E=B1F=
| 5 |
| 6 |
∴由余弦定理得cos∠EB1F=
| 2 |
| 5 |
即直线AM和CN所成角的大小为arccos
| 2 |
| 5 |
(2)根据中位线定理可知MN∥A1B,NP∥C1B
∴MN∥平面A1C1B,NP∥平面A1C1B,MN∩NP=P
∴平面A1C1B∥平面MNP,
而B1D⊥平面A1C1B,
所以B1D⊥面PMN;
(3)S△MNP=
| ||
| 2 |
| 3 |
| 2 |

设点A到平面PMN的距离为h
∴VA-MNP=VP-MNA
即
| 1 |
| 3 |
| 1 |
| 3 |
∴h=
| 3 |
点评:本小题主要考查异面直线所成的角,以及线面垂直的判定和点面距离的度量,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
在棱长为2的正方体AC1中,G是AA1的中点,则BD到平面GB1D1的距离是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成的角的余弦值等于( )
如图,在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成的角的余弦值等于( ) (理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F.
(理科)如图,在棱长为1的正方体A'C中,过BD及B'C'的中点E作截面BEFD交C'D'于F. (2007•上海)如图,在棱长为2的正方体ABCD-A'B'C'D'中,E,F分别是A'B'和AB的中点,求异面直线A'F与CE所成角的大小 (结果用反三角函数值表示).
(2007•上海)如图,在棱长为2的正方体ABCD-A'B'C'D'中,E,F分别是A'B'和AB的中点,求异面直线A'F与CE所成角的大小 (结果用反三角函数值表示).