题目内容
（2007•上海）如图，在棱长为2的正方体ABCD-A'B'C'D'中，E，F分别是A'B'和AB的中点，求异面直线A'F与CE所成角的大小 （结果用反三角函数值表示）．分析：（法一）如图建立空间直角坐标系，把要求的角转化为向量
，
的夹角，用坐标运算求解；（法二）：连接EB，可证A'FBE是平行四边形，可得异面直线A'F与CE所成的角就是CE与EB所成的角，在Rt△CEB中，可得tan∠CEB=
，由反正切可得所求的角．
| A′F |
| CE |
2
| ||
| 5 |
解答：解：（法一）如图建立空间直角坐标系． …（2分）
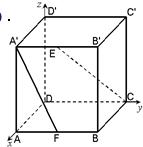
由题意可知A′（2，0，2），C（0，2，0），E（2，1，2），F（2，1，0）．
∴
=( 0，1，-2 )，
=( 2，-1，2 )．…（6分）
设直线A′F与CE所成角为θ，
则cosθ=
=
=
． …（10分）
∴θ=arccos
，
即异面直线A'F与CE所成角的大小为arccos
． …（12分）
（法二）：连接EB，…（2分）
∵A'E∥BF，且A'E=BF，∴A'FBE是平行四边形，则A'F∥EB，
∴异面直线A'F与CE所成的角就是CE与EB所成的角． …（6分）
由CB⊥平面ABB'A'，得CB⊥BE．
在Rt△CEB中，CB=2，BE=
，
则tan∠CEB=
，…（10分）
∴∠CEB=arctan
．
∴异面直线A'F与CE所成角的大小为arctan
． …（12分）
由题意可知A′（2，0，2），C（0，2，0），E（2，1，2），F（2，1，0）．
∴
| A′F |
| CE |
设直线A′F与CE所成角为θ，
则cosθ=
|
| ||||
|
|
| 5 | ||
|
| ||
| 3 |
∴θ=arccos
| ||
| 3 |
即异面直线A'F与CE所成角的大小为arccos
| ||
| 3 |
（法二）：连接EB，…（2分）
∵A'E∥BF，且A'E=BF，∴A'FBE是平行四边形，则A'F∥EB，
∴异面直线A'F与CE所成的角就是CE与EB所成的角． …（6分）
由CB⊥平面ABB'A'，得CB⊥BE．
在Rt△CEB中，CB=2，BE=
| 5 |
则tan∠CEB=
2
| ||
| 5 |
∴∠CEB=arctan
2
| ||
| 5 |
∴异面直线A'F与CE所成角的大小为arctan
2
| ||
| 5 |
点评：本题考查异面直线所成的角，涉及反三角函数的应用，属中档题．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
（2007•上海）下列四个函数中，图象如图所示的只能是（ ）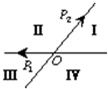
（2007•上海）如图，平面内的两条相交直线OP1和OP2将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ（不包括边界）．若
（2007•上海模拟）2005年1月6日《文汇报》载当日我国人口达到13亿，如图为该报提供的我国人口统计数据．2000年第五次全国人口普查后，专家们估算我国人口数的峰值为16亿，如果我国的人口增长率维持在最近几年的水平，那么，我国人口数大致在哪一年左右达到峰值（ ）
（2007•上海模拟）一个多面体的直观图，前视图（正前方观察），俯视图（正上方观察），侧视图（左侧正前方观察）如图所示．