题目内容
(本小题满分12分)

已知点 为圆
为圆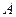 :
: 上任意一点,点
上任意一点,点 (-1,0),线段
(-1,0),线段 的垂直平分线和线段
的垂直平分线和线段 相交于点
相交于点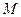 .
.
(Ⅰ)求点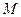 的轨迹
的轨迹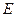 的方程;
的方程;
(Ⅱ)已知点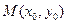 为曲线E上任意一点,
为曲线E上任意一点,
求证:点 关于直线
关于直线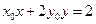 的对称点为定点,并求出该定点的坐标.
的对称点为定点,并求出该定点的坐标.

已知点
 为圆
为圆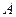 :
: 上任意一点,点
上任意一点,点 (-1,0),线段
(-1,0),线段 的垂直平分线和线段
的垂直平分线和线段 相交于点
相交于点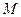 .
.(Ⅰ)求点
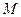 的轨迹
的轨迹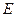 的方程;
的方程;(Ⅱ)已知点
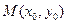 为曲线E上任意一点,
为曲线E上任意一点,求证:点
 关于直线
关于直线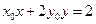 的对称点为定点,并求出该定点的坐标.
的对称点为定点,并求出该定点的坐标.M的轨迹E的方程为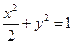 ,
,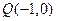
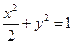 ,
,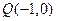
解:
(1)连结MB,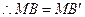 ,
,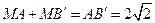
故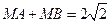 ,而
,而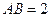
 点M的轨迹是以A、B为焦点且长轴长为
点M的轨迹是以A、B为焦点且长轴长为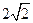 的椭圆
的椭圆
 点M的轨迹E的方程为
点M的轨迹E的方程为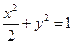 --------------------4分
--------------------4分
(2)证明:设点 关于直线
关于直线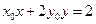 的对称点为
的对称点为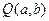
所以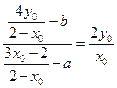 ,即
,即
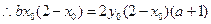 ,
,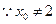
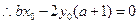

因为上式对任意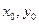 成立,故
成立,故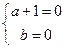

所以对称点为定点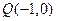 .
.
(1)连结MB,
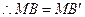 ,
,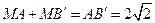
故
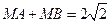 ,而
,而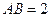
 点M的轨迹是以A、B为焦点且长轴长为
点M的轨迹是以A、B为焦点且长轴长为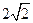 的椭圆
的椭圆 点M的轨迹E的方程为
点M的轨迹E的方程为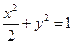 --------------------4分
--------------------4分(2)证明:设点
 关于直线
关于直线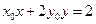 的对称点为
的对称点为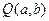
所以
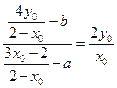 ,即
,即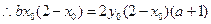 ,
,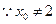
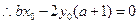

因为上式对任意
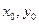 成立,故
成立,故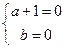

所以对称点为定点
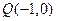 .
. 
练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
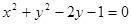 关于直线
关于直线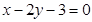 对称的圆方程是( )
对称的圆方程是( )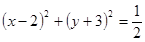
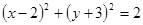
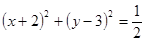
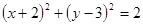
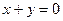 上一点P作圆
上一点P作圆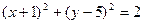 的两条切线
的两条切线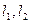 ,A,B为切点,当直线
,A,B为切点,当直线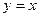 对称时,
对称时,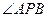 =( )
=( )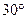
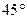
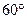
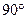
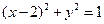 都相切,则双曲线C的离心率是
都相切,则双曲线C的离心率是 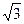 ,则
,则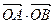 =
= 与圆
与圆 相切,则实数
相切,则实数 等于
等于



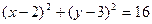 交于P、Q两点,若A恰为PQ的中点,则l的方程为
交于P、Q两点,若A恰为PQ的中点,则l的方程为



 的圆心
的圆心 ,且与直线
,且与直线 垂直的直线方程是 .
垂直的直线方程是 .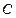 的参数方程为
的参数方程为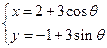 (
(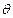 为参数),直线
为参数),直线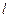 的方程为
的方程为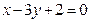 ,则曲线
,则曲线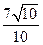 的点的
的点的 个数为
个数为