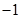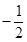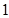题目内容
一同学在电脑中打出如下若干个圆（图中●表示实心圆，○表示空心圆）：
○●○○●○○○●○○○○●○○○○○●若将此若干个圆依次复制得到一系列圆，那么在前2006个圆中有（ ）个实心圆。
○●○○●○○○●○○○○●○○○○○●若将此若干个圆依次复制得到一系列圆，那么在前2006个圆中有（ ）个实心圆。
| A．60 | B．61 | C．62 | D．63 |
B
试题分析：先找规律，研究圆的总数，再看第2006个圆在第几组内，由实心球的个数等于组数求解．解：观察一下，以“实心个数加空心个数”为一组，这样圆的总数是： 2+3+4+…+=2006，而（2+63）*62/2=2015，说明第2006个圆在第62组中，因实心球排在每一组的末尾，所以第62组没有实心球．空心球的个数=组数2010个球中空心的有：61个．故答案是B
点评：本题主要考查归纳推理，解答关键是从圆的个数的变化规律中寻求规律，后建立数列模型解决问题．
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
个小球，将它们任意分成两堆，求出这两堆小球球数的乘积，再将其中一堆小球任意分成两堆，求出这两堆小球球数的乘积，如此下去，每次都任选一堆，将这堆小球任意分成两堆，求出这两堆小球球数的乘积，直到不能再分为止，则所有乘积的和为 ．
,
,
,…, 照此规律，
（
N
）.
，结论是：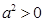
，那么这个演绎推理出错在：（ ）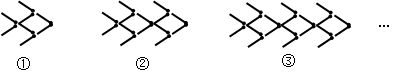
个“金鱼”图需要火柴棒的根数为 
B．
C．
D．
则由(2) 有体积关系:
,
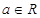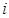是虚数单位，则当
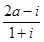是纯虚数时，实数
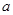为
