题目内容
设n∈N*,f(n)=1+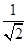 +
+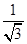 +…+
+…+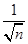 ,试比较f(n)与
,试比较f(n)与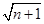 的大小.
的大小.
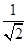 +
+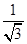 +…+
+…+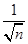 ,试比较f(n)与
,试比较f(n)与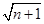 的大小.
的大小.当n=1,2时f(n)<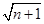 ;当n≥3时f(n)>
;当n≥3时f(n)>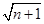 .
.
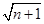 ;当n≥3时f(n)>
;当n≥3时f(n)>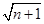 .
.当n=1,2时f(n)<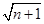 ;
;
当n≥3时f(n)>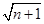 .
.
下面用数学归纳法证明:
①当n=3时,显然成立;
②假设当n=k(k≥3,k∈N?)时,即f(k)> ,那么,当n=k+1时,f(k+1)>
,那么,当n=k+1时,f(k+1)> +
+ =
= >
> =
= ,即n=k+1时,不等式也成立.
,即n=k+1时,不等式也成立.
由①②知,对任何n≥3,n∈N?不等式成立.
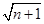 ;
;当n≥3时f(n)>
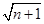 .
.下面用数学归纳法证明:
①当n=3时,显然成立;
②假设当n=k(k≥3,k∈N?)时,即f(k)>
 ,那么,当n=k+1时,f(k+1)>
,那么,当n=k+1时,f(k+1)> +
+ =
= >
> =
= ,即n=k+1时,不等式也成立.
,即n=k+1时,不等式也成立.由①②知,对任何n≥3,n∈N?不等式成立.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 成立.
成立.
 的第二步中,当
的第二步中,当 时等式左边与
时等式左边与 时的等式左边的差等于 .
时的等式左边的差等于 .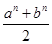 ≥
≥ n(a,b是非负实数,n∈N+)时,假设n
n(a,b是非负实数,n∈N+)时,假设n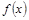 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且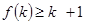 成立时,总可推出
成立时,总可推出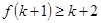 成立”,那么,下列命题总成立的是 ( )
成立”,那么,下列命题总成立的是 ( )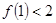 成立,则
成立,则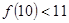 成立
成立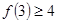 成立,则当
成立,则当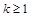 时,均有
时,均有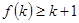 成立
成立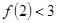 成立,则
成立,则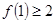 成立
成立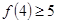 成立,则当
成立,则当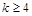 时,均有
时,均有 ;
;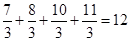 ;
; ;……
;…… 且
且 时,
时, .(最后结果用
.(最后结果用 表示)
表示)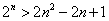 ”对于
”对于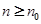 的正整数
的正整数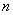 均成立”时,第一步证明中的起始值
均成立”时,第一步证明中的起始值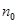 应取( )
应取( )