题目内容
如图,函数y=f(x)的图象为折线OAB,设g(x)=f[f(x)],则满足方程g(x)=x的根的个数为( )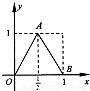
A.2个
B.4个
C.6个
D.8个
【答案】分析:先根据图象求得函数f(x),再根据g(x)=f[f(x)],求得函数g(x),画出函数g(x)的图象,然后根据方程g(x)=x的根的个数,即为函数y=x与函数y=g(x)的图象交点的个数,利用图象法得到答案.
解答:解:依题意得f(x)=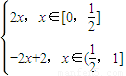 ,
,
g(x)=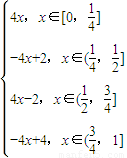
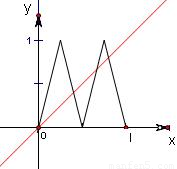
在同一坐标系中画出函数y=x与函数y=g(x)的图象如图所示:
由图可知函数y=x与函数y=g(x)的图象共有4个交点,
即满足方程g(x)=x的根的个数是4个,
故选B.
点评:本题主要考查通过图象求函数解析式和根的存在性及根的个数判断的问题,还涉及了分段函数,利用转化思想,将根的个数问题,转化为函数图象交点个数问题,是解答本题的关键.
解答:解:依题意得f(x)=
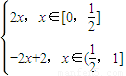 ,
,
g(x)=
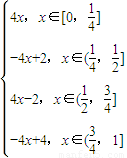
在同一坐标系中画出函数y=x与函数y=g(x)的图象如图所示:
由图可知函数y=x与函数y=g(x)的图象共有4个交点,
即满足方程g(x)=x的根的个数是4个,
故选B.
点评:本题主要考查通过图象求函数解析式和根的存在性及根的个数判断的问题,还涉及了分段函数,利用转化思想,将根的个数问题,转化为函数图象交点个数问题,是解答本题的关键.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
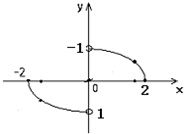 如图,函数y=f(x)的图象是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )
如图,函数y=f(x)的图象是中心在原点,焦点在x轴上的椭圆的两段弧,则不等式f(x)<f(-x)+x的解集为( )A、{
| ||||||||
B、{x|-2≤x<
| ||||||||
C、{x|-
| ||||||||
D、{x|-
|
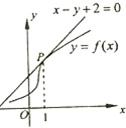 8、如图,函数y=f(x)的图象在点P处的切线方程为x-y+2=0,则f(1)+f′(1)=( )
8、如图,函数y=f(x)的图象在点P处的切线方程为x-y+2=0,则f(1)+f′(1)=( )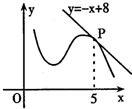 (文)如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=
(文)如图,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)= (2012•茂名一模)如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
(2012•茂名一模)如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题: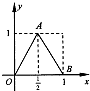 (2013•金华模拟)如图,函数y=f(x)的图象为折线OAB,设g(x)=f[f(x)],则满足方程g(x)=x的根的个数为( )
(2013•金华模拟)如图,函数y=f(x)的图象为折线OAB,设g(x)=f[f(x)],则满足方程g(x)=x的根的个数为( )