题目内容
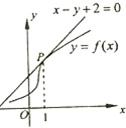8、如图，函数y=f（x）的图象在点P处的切线方程为x-y+2=0，则f（1）+f′（1）=（ ）分析：观察图象可得点P（1，f（1））在切线x-y+2=0上，故可求出f（1）；由导数的几何意义可得图象在点P处的切线的斜率k=
f′（1），由此求出f′（1），故问题得解．
f′（1），由此求出f′（1），故问题得解．
解答：解：∵点P（1，f（1））在切线x-y+2=0上，
∴1-f（1）+2=0，
解得f（1）=3；
又∵f′（1）=k=1，
∴f（1）+f′（1）=4，
故选D．
∴1-f（1）+2=0，
解得f（1）=3；
又∵f′（1）=k=1，
∴f（1）+f′（1）=4，
故选D．
点评：解决切线问题时，要充分利用导数的几何意义结合数形结合的知识来解决．
练习册系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
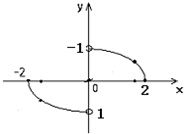如图，函数y=f（x）的图象是中心在原点，焦点在x轴上的椭圆的两段弧，则不等式f（x）＜f（-x）+x的解集为（ ）A、{
| ||||||||
B、{x|-2≤x＜
| ||||||||
C、{x|-
| ||||||||
D、{x|-
|
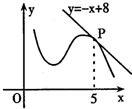（文）如图，函数y=f（x）的图象在点P处的切线方程是y=-x+8，则f（5）+f′（5）=
（2012•茂名一模）如图是函数y=f（x）的导函数y=f′（x）的图象，给出下列命题：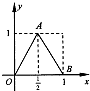
（2013•金华模拟）如图，函数y=f（x）的图象为折线OAB，设g（x）=f[f（x）]，则满足方程g（x）=x的根的个数为（ ）