题目内容
5.若关于x的方程|loga|x+b||=b(a>0,a≠1),有且只有两个解,则( )| A. | b=1 | B. | b=0 | C. | b>1 | D. | b>0 |
分析 由题意得loga|x+b|=b,或loga|x+b|=-b;从而分类讨论以确定方程解的个数即可.
解答 解:∵|loga|x+b||=b,
∴loga|x+b|=b,或loga|x+b|=-b;
①若b=0,则x=±1,成立;
②若b>0,则|x+b|=ab,|x+b|=a-b;
此时有四个解;
故不成立;
故选B.
点评 本题考查了绝对值方程的求解及对数函数与指数函数的性质应用,同时考查了分类讨论的思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
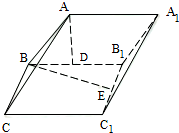
 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=45°,PD⊥平面ABCD,PD=AD=1,点E为AB上一点,且$\frac{AE}{AB}$=k,点F为PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=45°,PD⊥平面ABCD,PD=AD=1,点E为AB上一点,且$\frac{AE}{AB}$=k,点F为PD中点.