Question

设椭圆的方程为

x2

a2

+

y2

b2

=1（a＞b＞0），线段PQ是过左焦点F且不与x轴垂直的焦点弦．若在左准线上存在点R，使△PQR为正三角形，求椭圆的离心率e的取值范围，并用e表示直线PQ的斜率．

Answer 1

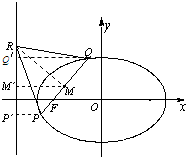
分析：如图，设线段PQ 的中点为M．过点 P、M、Q 分别作准线的垂线，垂足分别为 P′、M′、Q′，利用梯形的中位线定理和椭圆的第二定义可得：|MM′|=

1

2

(|PP′|+|QQ′|)=

1

2

(

|PF|

e

+

|QF|

e

)=

|PQ|

2e

．假设存在点 R，利用正三角形的性质可得：|RM|=

3

2

|PQ|，且|MM′|＜|RM|，即

|PQ|

2e

＜

3 |PQ|

2

，即可得到离心率的取值范围．于是cos∠RMM′=

|MM′|

|RM|

=

|PQ|

2e

•

2

3 |PQ|

=

1

3 e

．故cot∠RMM′=

1

3e2-1

．若|PF|＜|QF|（如图），可得k_PQ=tan∠QFx=tan∠FMM′=cot∠RMM′．即可得出．

解答：解：如图，设线段PQ 的中点为M．
过点 P、M、Q 分别作准线的垂线，垂足
分别为 P′、M′、Q′，则|MM′|=

1

2

(|PP′|+|QQ′|)=

1

2

(

|PF|

e

+

|QF|

e

)=

|PQ|

2e

．
假设存在点 R，则|RM|=

3

2

|PQ|，且|MM′|＜|RM|，即

|PQ|

2e

＜

3 |PQ|

2

，
∴e＞

3

3

．
于是，cos∠RMM′=

|MM′|

|RM|

=

|PQ|

2e

•

2

3 |PQ|

=

1

3 e

．故cot∠RMM′=

1

3e2-1

．
若|PF|＜|QF|（如图），则k_PQ=tan∠QFx=tan∠FMM′=cot∠RMM′=

1

3e2-1

．
当e＞

3

3

 时，过点F 作斜率为

1

3e2-1

 的焦点弦PQ，它的中垂线交左准线于 R，
由上述知，|RM|=

3

2

|PQ|． 故△PQR 为正三角形．
若|PF|＞|QF|，则由对称性得kPQ=-

1

3e2-1

．
又 e＜1，所以，椭圆的离心率 e 的取值范围是(

3

3

，1)，直线 PQ 的斜率为±

1

3e2-1

．

点评：本题综合考查了椭圆的第二定义、梯形的中位线定理、正三角形的性质、直线的斜率、分类讨论等基础知识与基本技能，考查了推理能力和计算能力，属于难题．