题目内容
已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是( )
A. =1.23x+4 =1.23x+4 | B. =1.23x+5 =1.23x+5 | C. =1.23x+0.08 =1.23x+0.08 | D. =0.08x+1.23 =0.08x+1.23 |
C
解析试题分析:解:设回归直线方程为 =1.23x+a,∵样本点的中心为(4,5),∴5=1.23×4+a,∴a=0.08,∴回归直线方程为
=1.23x+a,∵样本点的中心为(4,5),∴5=1.23×4+a,∴a=0.08,∴回归直线方程为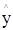 =1.23x+0.08,故选C.
=1.23x+0.08,故选C.
考点:线性回归方程
点评:本题考查线性回归方程,考查学生的计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
对于线性相关系数 ,叙述正确的是
,叙述正确的是
A.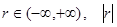 越大,相关程度越大,反之相关程度越小 越大,相关程度越大,反之相关程度越小 |
B. 越大,相关程度越大,反之相关程度越小 越大,相关程度越大,反之相关程度越小 |
C.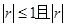 越接近1,相关程度越大 越接近1,相关程度越大 |
| D.以上说法都不对 |
已知一组正数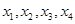 的方差为
的方差为 ,则数据
,则数据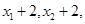
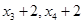 的平均数为( )
的平均数为( )
| A.2 | B.4 | C.-2 | D.不确定 |
一批灯泡400只,其中20 W、40 W、60 W的数目之比为4∶3∶1,现用分层抽样的方法产生一个容量为40的样本,三种灯泡依次抽取的个数为( )
| A.20 ,10 , 10 | B.15 , 20 , 5 | C.20, 5, 15 | D.20, 15, 5 |
若许昌学院共有在校大学生16050名,其中专科生4500人,本科生9750人,研究生1800人,
现在需要采用分层抽样的方法调查学生的家庭情况,已知从专科生抽取了60人,则需要从本科生、研究
生两类学生分别抽取多少人 ( )
| A.130 ,24 | B.260,24 | C.390,48 | D.130,36 |
为了了解某校高三学生的视力情况,随机地抽查了该校100名高三学生,得到学生视力频率分布直方图,如右图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频率成等差数列.设最大频率为a;视力在4.6到5.0之间的学生人数为b,则a、b的值分别为
| A.0.27,78 | B.0.27,83 |
| C.2.7,78 | D.2.7,83 |
在独立性检验中,统计量 有两个临界值:3.841和6.635;当
有两个临界值:3.841和6.635;当 >3.841时,有95%的把握说明两个事件有关,当
>3.841时,有95%的把握说明两个事件有关,当 >6.635时,有99%的把握说明两个事件有关,当
>6.635时,有99%的把握说明两个事件有关,当
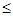 3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的
3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的 =20.87,根据这一数据分析,认为打鼾与患心脏病之间
=20.87,根据这一数据分析,认为打鼾与患心脏病之间
| A.有95%的把握认为两者有关 | B.约有95%的打鼾者患心脏病 |
| C.有99%的把握认为两者有关 | D.约有99%的打鼾者患心脏病 |
已知某产品的广告费用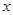 万元与销售额
万元与销售额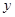 万元的统计数据如表所示:
万元的统计数据如表所示:
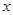 (万元) (万元) | 0 | 1 | 3 | 4 |
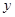 (万元) (万元) | 2.2 | 4.3 | 4.8 | 6.7 |
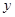 与
与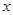 线性相关,且
线性相关,且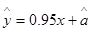 ,则据此模型预报广告费用为6万元时销售额为
,则据此模型预报广告费用为6万元时销售额为A. 2.6万元 B. 8.3万元 C. 7.3万元 D. 9.3万元