题目内容
已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程;
(2)从圆C外一点P(x1,y1)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
(1)y=(2± )x或x+y+1=0或x+y-3=0;(2)
)x或x+y+1=0或x+y-3=0;(2)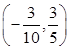 .
.
解析试题分析:(1)圆的方程化为标准方程,求出圆心与半径,再分类讨论,设出切线方程,利用直线是切线建立方程,即可得出结论;
(2)先确定P的轨迹方程,再利用要使|PM|最小,只要|PO|最小即可.
试题解析:(1)将圆C配方得:(x+1)2+(y-2)2=2.
①当直线在两坐标轴上的截距为零时,设直线方程为y=kx,由直线与圆相切得:y=(2± )x.
)x.
②当直线在两坐标轴上的截距不为零时,设直线方程为x+y-a=0,由直线与圆相切得:x+y+1=0或x+y-3=0.故切线方程为y=(2± )x或x+y+1=0或x+y-3=0.
)x或x+y+1=0或x+y-3=0.
(2)由|PO|=|PM|,得: =(x1+1)2+(y1-2)2-2⇒2x1-4y1+3=0.即点P在直线l:2x-4y+3=0上,当|PM|取最小值时即|OP|取得最小值,直线OP⊥l.
=(x1+1)2+(y1-2)2-2⇒2x1-4y1+3=0.即点P在直线l:2x-4y+3=0上,当|PM|取最小值时即|OP|取得最小值,直线OP⊥l.
∴直线OP的方程为:2x+y=0.解方程组 得P点坐标为
得P点坐标为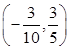 .
.
考点:直线和圆的方程的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
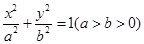 上的点到椭圆右焦点
上的点到椭圆右焦点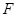 的最大距离为
的最大距离为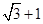 ,离心率
,离心率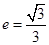 ,直线
,直线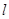 过点
过点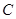 交于
交于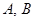 两点.
两点.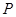 ,使得当
,使得当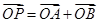 成立?若存在,求出所有点
成立?若存在,求出所有点 经过直线
经过直线 与直线
与直线 的交点
的交点 ,且垂直于直线
,且垂直于直线 .
. 对称的直线方程.
对称的直线方程.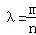 ,△BDM和△ABN的面积分别为S1和S2.
,△BDM和△ABN的面积分别为S1和S2.