题目内容
设m是平面α内的一条定直线,P是平面α外的一个定点,动直线n经过点P且与m成30°角,则直线n与平面α的交点Q的轨迹是
- A.圆
- B.椭圆
- C.双曲线
- D.抛物线
C
分析:过点P作PO⊥α,以点O为坐标原点,OP为z轴,以定直线m为y轴,建立如图所示的空间直角坐标系,设出坐标,分别表示出直线AB与PM的方向向量,利用夹角公式即可得出.
解答:过点P作PO⊥α,以点O为坐标原点,OP为z轴,以定直线m为y轴,建立如图所示的空间直角坐标系.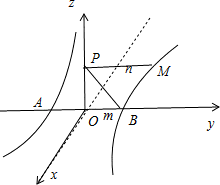
不妨设OP=1,∵∠PBO=30°,∴OB= .
.
则 P(0,0,1),B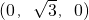 .
.
设点Q(x,y,0),则 ,取直线m的方向向量为
,取直线m的方向向量为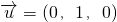 .
.
∵直线AB与PQ所成的角为30°,
∴cos30°=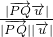 =
=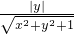 =
= ,
,
化为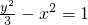 ,即为点Q的轨迹.
,即为点Q的轨迹.
故选C.
点评:熟练掌握通过建立如图所示的空间直角坐标系利用异面直线的夹角夹角公式求得轨迹的方法是解题的关键.
分析:过点P作PO⊥α,以点O为坐标原点,OP为z轴,以定直线m为y轴,建立如图所示的空间直角坐标系,设出坐标,分别表示出直线AB与PM的方向向量,利用夹角公式即可得出.
解答:过点P作PO⊥α,以点O为坐标原点,OP为z轴,以定直线m为y轴,建立如图所示的空间直角坐标系.
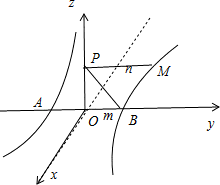
不妨设OP=1,∵∠PBO=30°,∴OB=
 .
.则 P(0,0,1),B
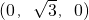 .
.设点Q(x,y,0),则
 ,取直线m的方向向量为
,取直线m的方向向量为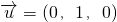 .
.∵直线AB与PQ所成的角为30°,
∴cos30°=
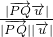 =
=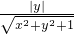 =
= ,
,化为
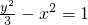 ,即为点Q的轨迹.
,即为点Q的轨迹.故选C.
点评:熟练掌握通过建立如图所示的空间直角坐标系利用异面直线的夹角夹角公式求得轨迹的方法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目