题目内容
(07年辽宁卷)(14分)
已知正三角形![]() 的三个顶点都在抛物线
的三个顶点都在抛物线![]() 上,其中
上,其中![]() 为坐标原点,设圆
为坐标原点,设圆![]() 是
是![]() 的内接圆(点
的内接圆(点![]() 为圆心)
为圆心)
(I)求圆![]() 的方程;
的方程;
(II)设圆![]() 的方程为
的方程为![]() ,过圆
,过圆![]() 上任意一点
上任意一点![]() 分别作圆
分别作圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,求
,求![]() 的最大值和最小值.
的最大值和最小值.
本小题主要考查平面向量,圆与抛物线的方程及几何性质等基本知识,考查综合运用解析几何知识解决问题的能力.
解析:(I)解法一:设![]() 两点坐标分别为
两点坐标分别为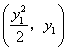 ,
,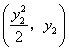 ,由题设知
,由题设知
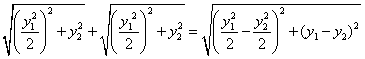 .
.
解得![]() ,
,
所以![]() ,
,![]() 或
或![]() ,
,![]() .
.
设圆心![]() 的坐标为
的坐标为![]() ,则
,则![]() ,所以圆
,所以圆![]() 的方程为
的方程为
![]() .
.
解法二:设![]() 两点坐标分别为
两点坐标分别为![]() ,
,![]() ,由题设知
,由题设知
![]() .
.
又因为![]() ,
,![]() ,可得
,可得![]() .即
.即
![]() .
.
由![]() ,
,![]() ,可知
,可知![]() ,故
,故![]() 两点关于
两点关于![]() 轴对称,所以圆心
轴对称,所以圆心![]() 在
在![]() 轴上.
轴上.
设![]() 点的坐标为
点的坐标为![]() ,则
,则![]() 点坐标为
点坐标为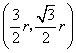 ,于是有
,于是有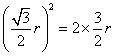 ,解得
,解得![]() ,所以圆
,所以圆![]() 的方程为
的方程为![]() .
.
(II)设![]() ,则
,则
![]() .
.
在![]() 中,
中,![]() ,由圆的几何性质得
,由圆的几何性质得
![]()
![]() ,
,![]() ,
,
所以![]() ,由此可得
,由此可得
![]() .
.
则![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
(07年辽宁卷理)(12分)
某企业准备投产一批特殊型号的产品,已知该种产品的成本![]() 与产量
与产量![]() 的函数关系式为
的函数关系式为
![]()
该种产品的市场前景无法确定,有三种可能出现的情况,各种情形发生的概率及产品价格![]() 与产量
与产量![]() 的函数关系式如下表所示:
的函数关系式如下表所示:
市场情形 | 概率 | 价格 |
好 | 0.4 |
|
中 | 0.4 |
|
差 | 0.2 |
|
设![]() 分别表示市场情形好、中差时的利润,随机变量
分别表示市场情形好、中差时的利润,随机变量![]() ,表示当产量为
,表示当产量为![]() ,而市场前景无法确定的利润.
,而市场前景无法确定的利润.
(I)分别求利润![]() 与产量
与产量![]() 的函数关系式;
的函数关系式;
(II)当产量![]() 确定时,求期望
确定时,求期望![]() ;
;
(III)试问产量![]() 取何值时,
取何值时,![]() 取得最大值.
取得最大值.
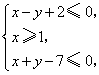 则
则