题目内容
已知函数f(x)＝2sin2(
＋x)－
cos2x－1，x∈[，
]，则f(x)的最小值为________．
＋x)－cos2x－1，x∈[，]，则f(x)的最小值为________．1
f(x)＝2sin2(＋x)－cos2x－1＝1－cos2(＋x)－cos2x－1＝－cos(＋2x)－cos2x＝sin2x－cos2x＝2sin(2x－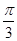
)，因为≤x≤，所以
≤2x－≤
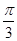，所以sin≤sin(2x－)≤sin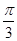，即
≤sin(2x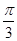－)≤1，所以1≤2sin(2x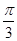－)≤2，即1≤f(x)≤2，所以f(x)的最小值为1．
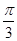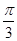＋x)－cos2x－1＝1－cos2(＋x)－cos2x－1＝－cos(＋2x)－cos2x＝sin2x－cos2x＝2sin(2x－)，因为≤x≤，所以≤2x－≤，所以sin≤sin(2x－)≤sin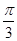，即≤sin(2x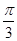－)≤1，所以1≤2sin(2x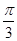－)≤2，即1≤f(x)≤2，所以f(x)的最小值为1．
练习册系列答案
寒假学与练系列答案
相关题目
为锐角，且有
，
，
的值是 .
的值. (2)求 
的值. 
sinωxcosωx－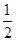
(ω>0)的最小正周期为π．
，f(
)＝
，求角C的大小．
个单位后得到函数F(x)的图象，则下列说法中正确的是( )
，
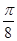]上的最大值和最小值分别为________．
＋α)＝
，则cos(
－2α)等于( )
（
）.
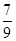
的最小正周期及
上的值域；
中，
，
.若
，求
则x , y的大小关系为( ) .
