题目内容
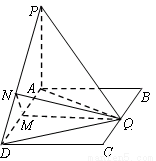
.(本小题满分12分)如图,在矩形 中,
中, ,又
,又 ⊥平面
⊥平面 ,
,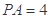 .
.
(Ⅰ)若在边 上存在一点
上存在一点 ,使
,使 ,
,
求 的取值范围;
的取值范围;
(Ⅱ)当边 上存在唯一点
上存在唯一点 ,使
,使 时,
时,
求二面角 的余弦值.
的余弦值.
【答案】
解法1:(Ⅰ)如图,连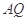 ,由于PA⊥平面ABCD,则由PQ⊥QD,必有
,由于PA⊥平面ABCD,则由PQ⊥QD,必有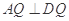 .
.
 ……2分
……2分
设 ,则
,则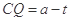 ,
,
在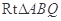 中,有
中,有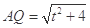 .
.
在 中,有
中,有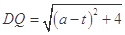 . ……4分
. ……4分
在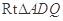 中,有
中,有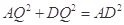 .
.
即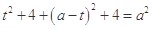 ,即
,即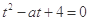 .
.
∴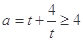 .
.
故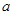 的取值范围为
的取值范围为 .
……6分
.
……6分
(Ⅱ)由(Ⅰ)知,当 ,
,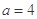 时,边BC上存在唯一点Q(Q为BC边的中点),使PQ⊥QD.
时,边BC上存在唯一点Q(Q为BC边的中点),使PQ⊥QD.
过Q作QM∥CD交AD于M,则QM⊥AD.
∵PA⊥平面ABCD,∴PA⊥QM.∴QM⊥平面PAD.
过M作MN⊥PD于N,连结NQ,则QN⊥PD.
∴∠MNQ是二面角A-PD-Q的平面角. ……8分
在等腰直角三角形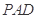 中,可求得
中,可求得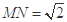 ,又
,又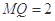 ,进而
,进而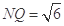 .
.
……10分
∴ .
.
故二面角A-PD-Q的余弦值为 .
……12分
.
……12分
【解析】略

练习册系列答案
相关题目