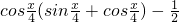题目内容
设函数y=f（x）满足f（2+x）=f（2-x），又f（x）在[2，+∞）是减函数，且f（a）≥f（0），则实数a的取值范围是（ ）
| A．a≥2 | B．a＜0 | C．0≤a≤4 | D．a＜0或a≥4 |
∵函数y=f（x）满足f（2+x）=f（2-x），
∴函数y=f（x）的对称轴为x=2
∵f（x）在[2，+∞）是减函数
∴f（x）在（-∞，2）是增函数
但a∈（-∞，2）时，f（a）≥f（0），则0≤a＜2
当a∈[2，+∞）时，f（a）≥f（0）=f（4），则2≤a≤4
∴实数a的取值范围是0≤a≤4
故选C．
∴函数y=f（x）的对称轴为x=2
∵f（x）在[2，+∞）是减函数
∴f（x）在（-∞，2）是增函数
但a∈（-∞，2）时，f（a）≥f（0），则0≤a＜2
当a∈[2，+∞）时，f（a）≥f（0）=f（4），则2≤a≤4
∴实数a的取值范围是0≤a≤4
故选C．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
