题目内容
(本小题满分12分)
已知数列(an}中,a1=2,前n项和Sn满足Sn+l-Sn=2n+1(n∈N*).
(Ⅰ)求数列(an}的通项公式an以及前n项和Sn;
(Ⅱ)令bn=2log2an+l,求数列{ }的前n项和Tn.
}的前n项和Tn.
已知数列(an}中,a1=2,前n项和Sn满足Sn+l-Sn=2n+1(n∈N*).
(Ⅰ)求数列(an}的通项公式an以及前n项和Sn;
(Ⅱ)令bn=2log2an+l,求数列{
 }的前n项和Tn.
}的前n项和Tn.解:(1)由Sm+1-Sn=2n+1得:an+1=2n+1. ……2分
又a1=2,所以an=2n(n∈N*). ……3分
从而Sn=2+22+…+2n=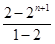 ……5分
……5分
==2n+1-2. ……6分
(2)因为bn=2log2an+1=2n+1, ……7分
所以 =
=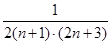 =
=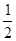 (
(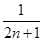 -
-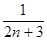 ), ……9分
), ……9分
于是Tn=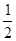 [(
[(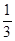 -
-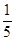 )+(
)+(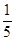 -
-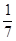 )+…+(
)+…+(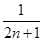 -
-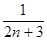 )] ……10分
)] ……10分
=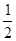 (
(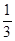 -
-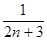 ) ……11分
) ……11分
=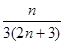 . ……12分
. ……12分
又a1=2,所以an=2n(n∈N*). ……3分
从而Sn=2+22+…+2n=
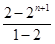 ……5分
……5分==2n+1-2. ……6分
(2)因为bn=2log2an+1=2n+1, ……7分
所以
 =
=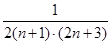 =
=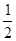 (
(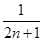 -
-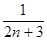 ), ……9分
), ……9分于是Tn=
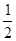 [(
[(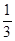 -
-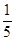 )+(
)+(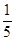 -
-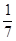 )+…+(
)+…+(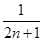 -
-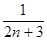 )] ……10分
)] ……10分=
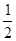 (
(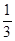 -
-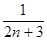 ) ……11分
) ……11分=
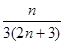 . ……12分
. ……12分略

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
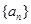 中,首项
中,首项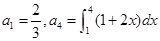 ,则公比为 。
,则公比为 。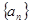 的公比为正数,且
的公比为正数,且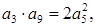
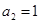 ,则
,则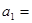 ()
()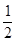
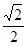
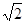
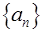 中,
中,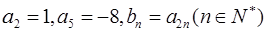 , 则数列
, 则数列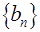 的
的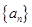 的前n项和为
的前n项和为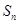 .已知
.已知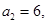
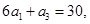 求
求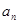 和
和 ,它的前
,它的前 项和为
项和为 ,则满足
,则满足 的最小
的最小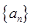 的前
的前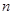 项和为
项和为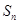 ,已知
,已知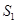 ,
,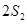 ,
,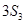 成等差数列,则
成等差数列,则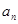 }中,已知
}中,已知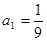 ,
,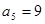 ,则
,则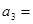 ( )
( )