题目内容
“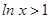 ”是“x>l"的( )
”是“x>l"的( )
| A.充要条件 | B.必要非充分条件 |
| C.充分非必要条件 | D.既不充分也不必要条件 |
C
解析试题分析:由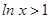 ,得
,得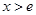 ,故
,故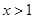 ,所以“
,所以“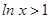 ”是“x>l"的充分不必要条件.
”是“x>l"的充分不必要条件.
考点:1、对数不等式的解法;2、充分必要条件.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
已知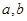 都是实数,那么“
都是实数,那么“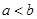 ”是“
”是“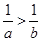 ”的( )条件
”的( )条件
| A.充分不必要 | B.必要不充分 |
| C.充要 | D.既不充分也不必要 |
已知命题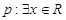 ,
,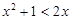 ;命题
;命题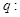 不等式
不等式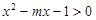 恒成立,那么( )
恒成立,那么( )
A.“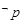 ”是假命题 ”是假命题 | B.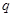 是真命题 是真命题 |
C.“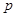 或 或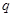 ”为假命题 ”为假命题 | D.“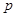 且 且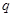 ”为真命题 ”为真命题 |
命题:“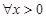 ,都有
,都有 ”的否定是( )
”的否定是( )
A.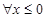 ,都有 ,都有 | B.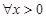 ,都有 ,都有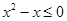 |
C.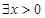 ,使得 ,使得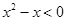 | D.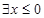 ,使得 ,使得 |
“实数 ”是“复数
”是“复数 (
( 为虚数单位)的模为
为虚数单位)的模为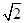 ”的( )
”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既非充分条件又不必要条件 |
已知命题 :复数
:复数 在复平面内所对应的点位于第四象限;命题
在复平面内所对应的点位于第四象限;命题 :
: ,
, ,则下列命题中为真命题的是( )
,则下列命题中为真命题的是( )
A. | B. | C. | D. |
已知命题 “
“ ,有
,有 成立”,则
成立”,则 为( )
为( )
A.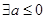 ,有 ,有 成立 成立 | B.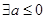 ,有 ,有 成立 成立 |
C. ,有 ,有 成立 成立 | D. ,有 ,有 成立 成立 |
已知命题p:?x∈R,cosx=;命题q:?x∈R,x2-x+1>0.则下列结论正确的是( )
A.命题 是假命题 是假命题 | B.命题 是真命题 是真命题 |
C.命题 是真命题 是真命题 | D.命题 是真命题 是真命题 |
命题“对任意的x∈R,x3﹣x2+1≤0”的否定是( )
| A.不存在x∈R,x3﹣x2+1≤0 | B.存在x∈R,x3﹣x2+1≤0 |
| C.存在x∈R,x3﹣x2+1>0 | D.对任意的x∈R,x3﹣x2+1>0 |