题目内容
(本题满分14分)如图多面体PQABCD由各棱长均为2的正四面体和正四棱锥拼接而成

(Ⅰ)证明PQ⊥BC;
(Ⅱ)若M为棱CQ上的点且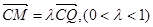 ,
,
求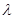 的取值范围,使得二面角P-AD-M为钝二面角。
的取值范围,使得二面角P-AD-M为钝二面角。

(Ⅰ)证明PQ⊥BC;
(Ⅱ)若M为棱CQ上的点且
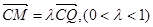 ,
, 求
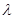 的取值范围,使得二面角P-AD-M为钝二面角。
的取值范围,使得二面角P-AD-M为钝二面角。(Ⅰ)见解析; (Ⅱ)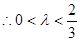
本试题主要是考查了立体几何中的线线垂直的证明,以及二面角的求解的综合运用。
(1)取AD中点E,连结PE,QE ……...2分

 均为正三角形得到线线垂直,然后利用线面垂直得到线线垂直的性质定理和判定定理的综合运用。
均为正三角形得到线线垂直,然后利用线面垂直得到线线垂直的性质定理和判定定理的综合运用。
(2)以正方形ABCD的中心O为原点,OF(F为AB的中点)为x轴,OQ为z轴,
建立空间坐标系,设出点的坐标,然后借助于向量的夹角公式表示二面角的平面角的大小。
解:(Ⅰ)取AD中点E,连结PE,QE ……...2分

 均为正三角形
均为正三角形
 AD
AD PE, AD
PE, AD QE
QE
 AD
AD 平面PEQ
平面PEQ
 AD
AD PQ 又AD//BC
PQ 又AD//BC
 PQ
PQ BC 。。。。。。。。。6分
BC 。。。。。。。。。6分
(Ⅱ)以正方形ABCD的中心O为原点,OF(F为AB的中点)为x轴,OQ为z轴,
建立空间坐标系, 则P(0,-2, ), Q(0,0,
), Q(0,0, ), B(1,1,0), C(-1,1,0),
), B(1,1,0), C(-1,1,0),
A(1,-1,0), D(-1,-1,0) 。。。。。。。。。。8分
平面PAD法向量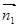 =(0,
=(0, ,1) 。。。。。。。。。。10分
,1) 。。。。。。。。。。10分

 =(0,2,0),
=(0,2,0), 
平面ADM的法向量 。。。。。。。。。12分
。。。。。。。。。12分

 。。。。。。。。。。。14分
。。。。。。。。。。。14分
(1)取AD中点E,连结PE,QE ……...2分

 均为正三角形得到线线垂直,然后利用线面垂直得到线线垂直的性质定理和判定定理的综合运用。
均为正三角形得到线线垂直,然后利用线面垂直得到线线垂直的性质定理和判定定理的综合运用。(2)以正方形ABCD的中心O为原点,OF(F为AB的中点)为x轴,OQ为z轴,
建立空间坐标系,设出点的坐标,然后借助于向量的夹角公式表示二面角的平面角的大小。
解:(Ⅰ)取AD中点E,连结PE,QE ……...2分

 均为正三角形
均为正三角形 AD
AD PE, AD
PE, AD QE
QE AD
AD 平面PEQ
平面PEQ AD
AD PQ 又AD//BC
PQ 又AD//BC PQ
PQ BC 。。。。。。。。。6分
BC 。。。。。。。。。6分(Ⅱ)以正方形ABCD的中心O为原点,OF(F为AB的中点)为x轴,OQ为z轴,
建立空间坐标系, 则P(0,-2,
 ), Q(0,0,
), Q(0,0, ), B(1,1,0), C(-1,1,0),
), B(1,1,0), C(-1,1,0), A(1,-1,0), D(-1,-1,0) 。。。。。。。。。。8分
平面PAD法向量
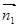 =(0,
=(0, ,1) 。。。。。。。。。。10分
,1) 。。。。。。。。。。10分
 =(0,2,0),
=(0,2,0), 
平面ADM的法向量
 。。。。。。。。。12分
。。。。。。。。。12分
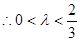 。。。。。。。。。。。14分
。。。。。。。。。。。14分
练习册系列答案
相关题目
 ,M是AB的中点,
,M是AB的中点,
 平面ABC;
平面ABC; 中,底面
中,底面 是正方形,其他四个侧面都是等边三角形,
是正方形,其他四个侧面都是等边三角形, 与
与 的交点为
的交点为 ,
, 为侧棱
为侧棱 上一点.
上一点.
 底面ABCD,
底面ABCD, DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.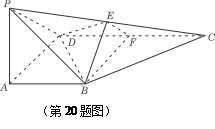
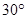 ,求k的取值范围.
,求k的取值范围. 中,
中, ,
, ,
, ,
, ,点
,点 是棱
是棱 的中点.
的中点.
 平面
平面 ;
; 的余弦值.
的余弦值. 中,面对角线
中,面对角线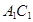 与体对角线
与体对角线 所成角等于
所成角等于

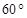

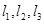 是空间三条不同的直线,则下列命题正确的是( )
是空间三条不同的直线,则下列命题正确的是( )
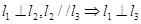
 共面
共面 共面
共面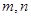 与平面
与平面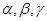 有以下三个命题
有以下三个命题
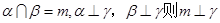
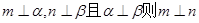 ,其中真命题有
,其中真命题有 ,直线
,直线 ,则下列四个命题:①
,则下列四个命题:①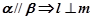 ;②
;②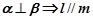 ;③
;③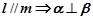 ;④
;④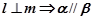 .其中正确的是( ).
.其中正确的是( ).